
已知函数 ,在点
,在点 处的切线方程是
处的切线方程是 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数 的值及
的值及 的解析式;
的解析式;
(2)若 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值;
(3)若关于x的不等式 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1)a=1,b=0,f(x)=xlnx;(2)tln (3)
(3)
【解析】
试题分析:(1)根据函数在点(e,f(e))处的切线方程是2x﹣y﹣e=0,可得f(e)=e,f′(e)=2,利用点(e,f(e))在函数f(x)=ax•lnx+b上,即可求实数a,b的值及f(x)的解析式;
(2)h(x)=f(x)+f(t﹣x)=xlnx+(t﹣x)ln(t﹣x),h(x)的定义域为(0,t),确定函数的单调性,从而可求h(x)的最小值;
(3)xlnx+(6﹣x)ln(6﹣x)=f(x)+f(6﹣x)=h(x),t=6时h(x)min=h(3)=6ln3=ln729,从而关于x的不等式xlnx+(6﹣x)ln(6﹣x)≥ln(k2﹣72k)对一切x∈(0,6)恒成立,转化为ln(k2﹣72k)≤ln729,解不等式,即可求得实数k的取值范围.
试题解析:(1)依题意有2e﹣f(e)﹣e=0,∴f(e)=e
∵f(x)=ax•lnx+b,∴f′(x)=alnx+a+b∴f′(e)=alne+a+b=2,∴2a+b=2,∴b=2﹣2a
∵点(e,f(e))在函数f(x)=ax•lnx+b上∴f(e)=aelne+b=ae+b=e
∴ae+2﹣2a=e,∴a=1∴b=0,∴f(x)=xlnx;
故实数a=1,b=0,f(x)=xlnx …(4分)
(2)h(x)=f(x)+f(t﹣x)=xlnx+(t﹣x)ln(t﹣x),
 的定义域为
的定义域为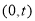 ;
; 
 增函数
增函数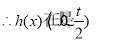 减函数
减函数
 (8分)
(8分)
(3)
由(2)知

 对一切
对一切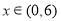 恒成立
恒成立


故实数 的取值范围
的取值范围 .(12分)
.(12分)
考点:利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.


科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试理科数学试卷(解析版) 题型:选择题
在一次反恐演习中,我方三架武装直升机分别从不同方位对同一目标发动攻击(各
发射一枚导弹),由于天气原因,三枚导弹命中目标的概率分别为 ,若至少有两枚导弹命中目标方可将其摧毁,则目标被摧毁的概率为( )
,若至少有两枚导弹命中目标方可将其摧毁,则目标被摧毁的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷(解析版) 题型:解答题
(本小题满分12分)若数列 满足前
满足前 项之和
项之和 且
且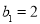 ,
,
(1)求数列 的通项公式
的通项公式
(2)证明: 是等差数列
是等差数列
(3)求 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期10月模块考试数学试卷(解析版) 题型:解答题
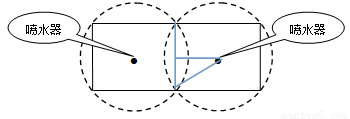
(本小题满分10分)如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器.已知喷水器的喷水区域是半径为5 m的圆.问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com