Question

13．V为矩形ABCD所在平面外一点，且VA=VB=VC=VD，$\overrightarrow{VP}$=$\frac{1}{3}$$\overrightarrow{VC}$，$\overrightarrow{VM}$=$\frac{2}{3}$$\overrightarrow{VB}$，$\overrightarrow{VN}$=$\frac{2}{3}$$\overrightarrow{VD}$，求证：VA∥平面PMN．

Answer 1

分析 如图所示，连接AC，延长PM，PN分别交CB、CD域点E，F，连接EF交AC于点O，连接OP．可得$\overrightarrow{MN}$=$\overrightarrow{VN}-\overrightarrow{VM}$=$\frac{2}{3}\overrightarrow{BD}$，同理可得$\overrightarrow{MN}$=$\frac{1}{2}\overrightarrow{EF}$，$\overrightarrow{BD}$=$\frac{3}{4}\overrightarrow{EF}$．于是$\overrightarrow{AO}=\frac{1}{3}\overrightarrow{AC}$．即可证明．

解答 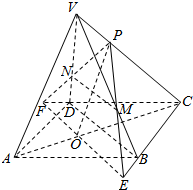证明：如图所示，
连接AC，延长PM，PN分别交CB、CD域点E，F，连接EF交AC于点O，连接OP．
$\overrightarrow{MN}$=$\overrightarrow{VN}-\overrightarrow{VM}$=$\frac{2}{3}（\overrightarrow{VD}-\overrightarrow{VB}）$=$\frac{2}{3}\overrightarrow{BD}$，
同理可得$\overrightarrow{MN}$=$\frac{1}{2}\overrightarrow{EF}$，
∴$\overrightarrow{BD}$=$\frac{3}{4}\overrightarrow{EF}$．
∴$\overrightarrow{AO}=\frac{1}{3}\overrightarrow{AC}$．
∴$\overrightarrow{VA}∥\overrightarrow{OP}$，
而VA?平面PMN，OP?平面PMN，
∴VA∥平面PMN．

点评 本题考查了向量共线定理、三角形法则、线面平行判定定理，考查了推理能力与计算能力，属于中档题．