
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 设α,β,γ的对边分别为a,b,c,不妨令α≤β≤γ,则a≤b≤c,则a+b>c,分别判断两个较小的边与最大边的差是否一定大于0,可得答案.
解答 解:∵α,β,γ是某三角形的三个内角,
设α,β,γ的对边分别为a,b,c,
不妨令α≤β≤γ,则a≤b≤c,则a+b>c.
则①中,sinα=$\frac{a}{2R}$,sinβ=$\frac{b}{2R}$,sinγ=$\frac{c}{2R}$;
则$\frac{a}{2R}$+$\frac{b}{2R}$>$\frac{c}{2R}$,故一定能构成三角形;
②中,sin2α=$\frac{{a}^{2}}{{4r}^{2}}$,sin2β=$\frac{{b}^{2}}{{4R}^{2}}$,sin2γ=$\frac{{c}^{2}}{{4R}^{2}}$,
由$\frac{{a}^{2}}{{4r}^{2}}$+$\frac{{b}^{2}}{{4R}^{2}}$>$\frac{{c}^{2}}{{4R}^{2}}$仅在a2+b2-c2>0,即cosγ>0时成立,故不一定能构成三角形.
③中,${cos}^{2}\frac{α}{2}$+${cos}^{2}\frac{β}{2}$-${cos}^{2}\frac{γ}{2}$=$\frac{cosα+cosβ-cosγ}{2}$+$\frac{1}{2}$>0恒成立.
恒成立,故一定能构成三角形,故③正确.
④中,当α=β=30°时γ=120°,tan$\frac{α}{2}$+tan$\frac{β}{2}$-tan$\frac{γ}{2}$<0,故不一定能构成三角形,
故①③正确,
故选:B.
点评 本题考查了构成三角形的条件,三角函数的图象和性质,是三角函数较为综合的考查,难度较大,属于难题


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{2}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
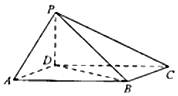 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1+p2+p3 | B. | 1-(1-p1)(1-p2)(1-p3) | C. | 1-p1p2p3 | D. | p1p2p3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com