
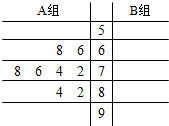
 某班A、B两组各有8名学生,他们期中考试的美术成绩如下:
某班A、B两组各有8名学生,他们期中考试的美术成绩如下:分析 (1)根据题目中的数据,补全茎叶图即可;
(2)计算A、B组两种成绩的平均数与方差和标准差,比较即可得出结论.
解答  解:(1)根据题目中的数据,补全茎叶图,如图所示;
解:(1)根据题目中的数据,补全茎叶图,如图所示;
(2)A组成绩的平均数是
$\overline{{x}_{A}}$=$\frac{1}{8}$(66+68+72+74+76+78+82+84)=75,
方差是
${{s}_{A}}^{2}$=$\frac{1}{8}$[(66-75)2+(68-75)2+(72-75)2+(74-75)2
+(76-75)2+(78-75)2+(82-75)2+(84-75)2]
=35,
标准差是sA=$\sqrt{35}$;
B组成绩的平均数是
$\overline{{x}_{B}}$=$\frac{1}{8}$(58+62+67+73+77+83+88+92)=75,
方差是
${{s}_{B}}^{2}$=$\frac{1}{8}$[(58-75)2+(62-75)2+(67-75)2+(73-75)2
+(77-75)2+(83-75)2+(88-75)2+(92-75)2]
=131.5,
标准差是sB=$\sqrt{131.5}$;
∵$\overline{{x}_{A}}$=$\overline{{x}_{B}}$,sA<sB,
∴A、B两组的水平相当,但A组比B组成绩更集中些.
点评 本题考查了茎叶图的应用问题,也考查了平均数、方差与标准差的计算与应用问题,是基础题目.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (120°,180°) | B. | (90°,120°) | C. | (60°,90°) | D. | (45°,60°) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | O (-2,0),r=2 | B. | O(-2,0),r=4 | C. | O(2,0),r=2 | D. | O(2,0),r=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(e)<f(3)<f(2) | B. | f(e)<f(2)<f(3) | C. | f(2)<f(3)<f(e) | D. | f(3)<f(2)<f(e) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com