
分析 (1)先求得点N关于直线y=x对称点M的坐标,可得圆M的方程,再根据圆心距大于两圆的半径之和,可得两圆相离.
(2)设∠PAB=2α,则∠APG=∠BPG=α,可得 $\frac{{S}_{△PBG}}{{S}_{△APG}}$=$\frac{\frac{1}{2}•PB•PG•sin∠BPG}{\frac{1}{2}•PA•PG•sin∠APG}$=$\frac{PB}{PG}$.设点P(x,y),求得PA2和 PB2的值,可得$\frac{PB}{PA}$的值,即为△PBG与△APG的面积之比.
解答 解:(1)由于点N($\frac{5}{3}$,-$\frac{5}{3}$)关于直线y=x对称点M(-$\frac{5}{3}$,$\frac{5}{3}$),
故圆M的方程为:(x+$\frac{5}{3}$)2+(y-$\frac{5}{3}$)2=r2.
把点D(-$\frac{1}{3}$,$\frac{5}{3}$)在圆M上,可得r2=$\frac{16}{9}$,故圆M的方程为:(x+$\frac{5}{3}$)2+(y-$\frac{5}{3}$)2=$\frac{16}{9}$.
可得圆N:(x-$\frac{5}{3}$)2+(y+$\frac{5}{3}$)2=$\frac{16}{9}$,N($\frac{5}{3}$,-$\frac{5}{3}$),
根据|MN|=$\sqrt{{(-\frac{5}{3}-\frac{5}{3})}^{2}{+(\frac{5}{3}+\frac{5}{3})}^{2}}$=$\frac{10\sqrt{2}}{3}$>$\frac{8}{3}$,故两圆相离.
(2)设∠PAB=2α,则∠APG=∠BPG=α,∴$\frac{{S}_{△PBG}}{{S}_{△APG}}$=$\frac{\frac{1}{2}•PB•PG•sin∠BPG}{\frac{1}{2}•PA•PG•sin∠APG}$=$\frac{PB}{PA}$.
设点P(x,y),则(x+$\frac{5}{3}$)2+(y-$\frac{5}{3}$)2=$\frac{16}{9}$.
PA2=(x+1)2+(y-$\frac{5}{3}$)2 =(x+1)2+$\frac{16}{9}$-(x+$\frac{5}{3}$)2=$\frac{-4}{3}$x;
PB2=(x-1)2+(y-$\frac{5}{3}$)2 =(x-1)2+$\frac{16}{9}$-(x+$\frac{5}{3}$)2=-$\frac{16}{3}$x;
∴$\frac{{PB}^{2}}{{PA}^{2}}$=4,∴$\frac{PB}{PA}$=2,即 $\frac{{S}_{△PBG}}{{S}_{△APG}}$=2.
点评 本题主要考查直线和圆的位置关系,圆和圆的位置关系,圆的切线性质,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
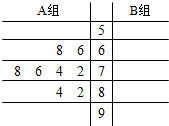 某班A、B两组各有8名学生,他们期中考试的美术成绩如下:
某班A、B两组各有8名学生,他们期中考试的美术成绩如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4] | B. | [-4,+∞) | C. | (-∞,4] | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=x0 | B. | f(x)=1,g(x)=$\frac{x}{x}$ | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
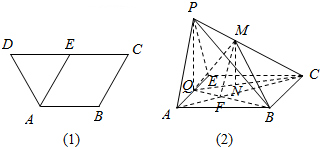 在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com