
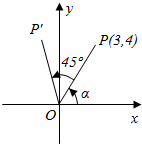
 如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.
如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标. 分析 利用两角和的正弦函数以及余弦函数即可求点P′的坐标.
解答 解:∵角α终边上一点P的坐标是(3,4),
∴32+42=52,
∴|OP|=5,
∴sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$,
设p′的坐标为(x,y),
∴y=|OP′|sin(α+45°)=5(sinαcos45°+cosαsin45°)=5($\frac{4}{5}$×$\frac{\sqrt{2}}{2}$+$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$)=$\frac{7\sqrt{2}}{2}$,
x=|OP′|cos(α+45°)=5(cosαcos45°-sinαsin45°)=5($\frac{3}{5}$×$\frac{\sqrt{2}}{2}$-$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$)=-$\frac{\sqrt{2}}{2}$,
∴p′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{7\sqrt{2}}{2}$).
点评 本题考查向量与三角函数的相结合,两角和与差的三角函数的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)有最大值-4 | B. | 函数f(x)有最小值-4 | ||
| C. | 函数f(x)有最大值-3 | D. | 函数f(x)有最小值-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com