
����Ŀ����֪һԪ���κ���f��x��=ax2+bx+c��a��0��c��0����ͼ����x����������ͬ�Ĺ����㣬����һ�������������Ϊ��c��0�����ҵ�0��x��cʱ������f��x����0��
��1����a=1�� ![]() ʱ���������ʽf��x����0�Ľ⣻
ʱ���������ʽf��x����0�Ľ⣻
��2���������ʽf��x����0�Ľ⣨��a��c��ʾ����
��3�����Զ��κ�����ͼ�������������������Ϊ����������ε����Ϊ8����a��ȡֵ��Χ��
��4��������ʽm2��2km+1+b+ac��0������k��[��1��1]���������ʵ��m��ȡֵ��Χ��
���𰸡�
��1���⣺��a=1�� ![]() ʱ��
ʱ�� ![]() ��
��
f��x����ͼ����x����������ͬ���㣬
�� ![]() ������һ����Ϊx2����
������һ����Ϊx2���� ![]() ����x2=1��
����x2=1��
�� f��x����0�Ľ⼯Ϊ ![]()
��2���⣺f��x����ͼ����x�����������㣬
��f��c��=0������һ����Ϊx2���� ![]() ��
��
�ֵ�0��x��cʱ������f��x����0���� ![]() ��
��
��f��x����0�Ľ⼯Ϊ ![]()
��3���⣺�ɣ�2����f��x����ͼ����������Ľ���ֱ�Ϊ ![]()
��������Ϊ����������ε����Ϊ ![]() ��
��
�� ![]() ��
�� ![]()
��4���⣺��f��c��=0����ac2+bc+c=0��
�֡�c��0����ac+b+1=0������11�֣�
Ҫʹm2��2km��0��������k��[��1��1]���������
��m��0ʱ��m�ݣ�2k��max=2
��m��0ʱ��m�ܣ�2k��min=��2
��m=0ʱ��02��2k0��������k��[��1��1]�����
�Ӷ�ʵ��m��ȡֵ��ΧΪ m�ܩ�2��m=0��m��2
����������1����a=1�� c = ![]() ʱ,f��x����x�����������㣬�ɴ������f��x����0�Ľ⼯����2��f��x����ͼ����x����������ͬ�Ľ��㣬���жϳ������Ĵ�С�ɵ�f��x����0�Ľ⼯����3���ɣ�2�����У��ó�f��x����������Ľ���ֱ�Ϊ ( c �� 0 ) �� (
ʱ,f��x����x�����������㣬�ɴ������f��x����0�Ľ⼯����2��f��x����ͼ����x����������ͬ�Ľ��㣬���жϳ������Ĵ�С�ɵ�f��x����0�Ľ⼯����3���ɣ�2�����У��ó�f��x����������Ľ���ֱ�Ϊ ( c �� 0 ) �� ( ![]() �� 0 ) �� ( 0 �� c ),��������ε�������ɴ����a��ȡֵ��Χ����4��f��c��=0��֪ac2+bc+c=0����c��0��֪ac+b+1=0���ɴ������ʵ��m��ȡֵ��Χ.
�� 0 ) �� ( 0 �� c ),��������ε�������ɴ����a��ȡֵ��Χ����4��f��c��=0��֪ac2+bc+c=0����c��0��֪ac+b+1=0���ɴ������ʵ��m��ȡֵ��Χ.
�����㾫�������ö��κ����ڱ������ϵ���ֵ�Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��![]() ʱ����
ʱ����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() �ϵݼ�����
�ϵݼ�����![]() ʱ��
ʱ��![]() �������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��
�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����g��x��=ax2��2ax+1+b��a��0��������[0��3]�������ֵ5����Сֵ1����f��x��= ![]() ��
��
��1����a��b��ֵ��
��2��������ʽf��x����k��0��x��[1��4]�Ϻ��������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() ������
������ ![]() ������a������a��0�����f��x��=g��x��h��x����
������a������a��0�����f��x��=g��x��h��x����
��1������f��x���ı���ʽ�������䶨����
��2���� ![]() ʱ������f��x����ֵ��
ʱ������f��x����ֵ��
��3���Ƿ������Ȼ��a��ʹ�ú���f��x����ֵ��ǡΪ ![]() �������ڣ���д������������������Ȼ��a�����ɵļ��ϣ��������ڣ���˵�����ɣ�
�������ڣ���д������������������Ȼ��a�����ɵļ��ϣ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʵ��x��y��m����|x��m|��|y��m|�����x��yԶ��m��
��1����x2��1��3Զ��0����x��ȡֵ��Χ��
��2����������������ȵ�����a��b��֤����a3+b3��a2b+ab2Զ��2ab ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2����a��2��x+a��4��
��1��������y=f��x��������[1��2]�ϵ���СֵΪ4��a����ʵ��a��ȡֵ��Χ��
��2���Ƿ��������m��n��ʹ�ù���x�IJ���ʽm��f��x����n�Ľ⼯ǡ��Ϊ[m��n]�������ڣ����m��n��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������Ϊ ![]() ����ԲC��
����ԲC�� ![]() +
+ ![]() =1��a��b��0������M��2��1����OΪ����ԭ�㣬ƽ����OM��ֱ��l����ԲC�ڲ�ͬ������A��B��
=1��a��b��0������M��2��1����OΪ����ԭ�㣬ƽ����OM��ֱ��l����ԲC�ڲ�ͬ������A��B�� 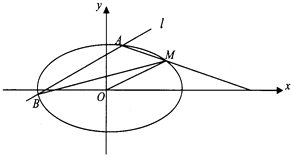
��1������ԲC�ķ��̣�
��2��֤����ֱ��MA��MB��x��Χ��һ�����������Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com