
【题目】解关于x的不等式x2﹣x﹣a(a﹣1)>0.
【答案】解:原不等式可化为:(x﹣a)(x+a﹣1)>0,
对应方程的根为x1=a,x2=1﹣a
(1)当 ![]() 时,有a<1﹣a,解可得x<a或x>1﹣a;
时,有a<1﹣a,解可得x<a或x>1﹣a;
(2)当 ![]() 时,a=1﹣a得x∈R且
时,a=1﹣a得x∈R且 ![]() ;
;
(3)当 ![]() 时,a>1﹣a,解可得x<1﹣a或x>a;
时,a>1﹣a,解可得x<1﹣a或x>a;
综合得:
(1)当 ![]() 时,原不等式的解集为(﹣∞,a)∪(1﹣a,+∞);
时,原不等式的解集为(﹣∞,a)∪(1﹣a,+∞);
(2)当 ![]() 时,原不等式的解集为
时,原不等式的解集为 ![]() ;
;
(3)当 ![]() 时,原不等式的解集为(﹣∞,1﹣a)∪(a,+∞).
时,原不等式的解集为(﹣∞,1﹣a)∪(a,+∞).
【解析】把不等式坐标利用十字相乘法分解因式:(x﹣a)(x+a﹣1)>0,然后对a值进行分类讨论:a与 ![]() 的大小关系三种情况,利用不等式取解集的方法分别求出各自的解集即可.
的大小关系三种情况,利用不等式取解集的方法分别求出各自的解集即可.
【考点精析】本题主要考查了解一元二次不等式的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 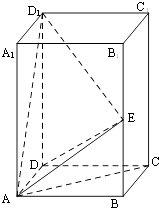
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高中入学新生的身高情况,从高一年级学生中按分层抽样共抽取了50名学生的身高数据,分组统计后得到了这50名学生身高的频数分布表:

(Ⅰ)在答题卡上作出这50名学生身高的频率分布直方图;
(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从身高在![]() 这6名学生中随机抽取3名,求至少抽到1名女生的概率.
这6名学生中随机抽取3名,求至少抽到1名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和定直线
和定直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作斜率不为0的任意一条直线与曲线
作斜率不为0的任意一条直线与曲线![]() 交于两点
交于两点![]() ,试问在
,试问在![]() 轴上是否存在一点
轴上是否存在一点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin(2ωx+ ![]() )+
)+ ![]() +b(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是
+b(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是 ![]() ,最小值是
,最小值是 ![]() .
.
(1)求ω、a、b的值;
(2)求f(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com