
【题目】已知动点![]() 到定点
到定点![]() 和定直线
和定直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作斜率不为0的任意一条直线与曲线
作斜率不为0的任意一条直线与曲线![]() 交于两点
交于两点![]() ,试问在
,试问在![]() 轴上是否存在一点
轴上是否存在一点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角三角形中,边a、b是方程x2﹣2 ![]() x+2=0的两根,角A、B满足:2sin(A+B)﹣
x+2=0的两根,角A、B满足:2sin(A+B)﹣ ![]() =0,求角C的度数,边c的长度及△ABC的面积.
=0,求角C的度数,边c的长度及△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.数据分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.
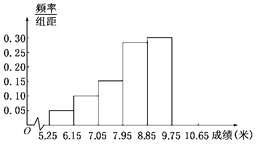
(I)求这次铅球测试成绩合格的人数;
(II)若参加测试的学生中9人成绩优秀,现要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知学生![]() 、
、![]() 的成绩均为优秀,求两人
的成绩均为优秀,求两人![]() 、
、![]() 至少有1人入选的概率.
至少有1人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面内有n(n∈N*)条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成f(n)个平面区域,则f(3)=;f(n)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com