
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 中点.
中点.
【解析】试题分析:(1)![]() 平面
平面![]() ,
, ![]() 为
为![]() 中
中![]() 边上的高,
边上的高, ![]() ,由线面垂直的判定定理能够证明
,由线面垂直的判定定理能够证明![]() 平面
平面![]() ;(2)连接
;(2)连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 是
是![]() 中点,
中点, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,由根据棱锥的体积公式能够求出三棱锥
,由根据棱锥的体积公式能够求出三棱锥![]() 的体积;(3)取
的体积;(3)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则因为
,则因为![]() 是
是![]() 的中点,先证明
的中点,先证明![]() ,再证明以
,再证明以![]() 平面
平面![]() ,可得
,可得![]() 面
面![]() ,即
,即![]() 与
与![]() 重合时符合题意.
重合时符合题意.
试题解析:(1)![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 又
又![]() ,
,![]() 平面
平面![]()
(2)![]() 是
是![]() 的中点,
的中点,![]() 到平面
到平面![]() 的距离
的距离![]() 等于点
等于点![]() 到平面
到平面![]() 距离的一半,即
距离的一半,即![]() =
=![]() ,又因为
,又因为![]() ,所以三棱锥
,所以三棱锥![]() ;
;
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则因为
,则因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,又因为
,又因为![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,因为ED//DQ,所以
,因为ED//DQ,所以![]() 面
面![]() .M为PB中点.
.M为PB中点.
【方法点晴】本题主要考查线面垂直的判定定理及棱锥的体积公式,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.


科目:高中数学 来源: 题型:
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中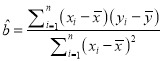 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 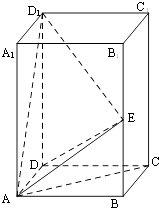
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 令Tn= ![]() ,称Tn为数列a1 , a2 , …,an的“理想数”,已知数列a1 , a2 , …,a502的“理想数”为2012,那么数列2,a1 , a2 , …,a502的“理想数”为( )
,称Tn为数列a1 , a2 , …,an的“理想数”,已知数列a1 , a2 , …,a502的“理想数”为2012,那么数列2,a1 , a2 , …,a502的“理想数”为( )
A.2010
B.2011
C.2012
D.2013
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,公比q≠1,等差数列{bn}满足b1=a1=3,b4=a2 , b13=a3 .
(1)求数列{an}与{bn}的通项公式;
(2)记cn=(﹣1)nbn+an , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和定直线
和定直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作斜率不为0的任意一条直线与曲线
作斜率不为0的任意一条直线与曲线![]() 交于两点
交于两点![]() ,试问在
,试问在![]() 轴上是否存在一点
轴上是否存在一点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com