
ЎҫМвДҝЎҝДііцЧвіө№«ЛҫПмУҰ№ъјТҪЪДЬјхЕЕөДәЕХЩЈ¬ТСВҪРш№әВтБЛ140Бҫҙҝөз¶ҜЖыіөЧчОӘФЛУӘіөБҫЈ¬ДҝЗ°ОТ№ъЦчБчҙҝөз¶ҜЖыіө°ҙРшәҪАпіМКэ![]() Ј®ЈЁөҘО»Јә№«АпЈ©·ЦОӘ3АаЈ¬јҙ
Ј®ЈЁөҘО»Јә№«АпЈ©·ЦОӘ3АаЈ¬јҙ![]() АаЈә
АаЈә![]() Ј¬
Ј¬![]() АаЈә
АаЈә![]() Ј¬
Ј¬ ![]() АаЈә
АаЈә![]() Ј¬ёГ№«Лҫ¶ФХв140БҫіөөДРРК»ЧЬАпіМҪшРРНіјЖЈ¬Ҫб№ыИзПВұнЈә
Ј¬ёГ№«Лҫ¶ФХв140БҫіөөДРРК»ЧЬАпіМҪшРРНіјЖЈ¬Ҫб№ыИзПВұнЈә
АаРН |
|
|
|
ТСРРК»ЧЬАпіМІ»і¬№э10Нт№«АпөДіөБҫКэ | 10 | 40 | 30 |
ТСРРК»ЧЬАпіМі¬№э10Нт№«АпөДіөБҫКэ | 20 | 20 | 20 |
ЈЁ1Ј©ҙУХв140БҫЖыіөЦРИОИЎТ»БҫЈ¬ЗуёГіөРРК»ЧЬАпіМі¬№э10Нт№«АпөДёЕВКЈ»
ЈЁ2Ј©№«ЛҫОӘБЛБЛҪвХвР©іөөД№ӨЧчЧҙҝцЈ¬ҫц¶ЁійИЎБЛ14БҫіөҪшРРіөҝц·ЦОцЈ¬°ҙұнЦРГиКцөДБщЦЦЗйҝцҪшРР·ЦІгійСщЈ¬ЙиҙУ![]() АаіөЦРійИЎБЛ
АаіөЦРійИЎБЛ![]() БҫіөЈ®
БҫіөЈ®
ўЩЗу![]() өДЦөЈ»
өДЦөЈ»
ўЪИз№ыҙУХв![]() БҫіөЦРЛж»ъСЎИЎБҪБҫіөЈ¬ЗуЗЎУРТ»БҫіөРРК»ЧЬАпіМі¬№э10Нт№«АпөДёЕВКЈ®
БҫіөЦРЛж»ъСЎИЎБҪБҫіөЈ¬ЗуЗЎУРТ»БҫіөРРК»ЧЬАпіМі¬№э10Нт№«АпөДёЕВКЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©ўЩ
Ј»ЈЁ2Ј©ўЩ![]() Ј»ўЪ
Ј»ўЪ![]() .
.
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©УЙұнҝЙөГЧЬАпіМі¬іц![]() Нт№«АпөДіөБҫКэ,ФЩЗуёЕВКЈ»ЈЁ2Ј©УЙ°ҙұИАэөД·ЦІгійСщҝЙөГ
Нт№«АпөДіөБҫКэ,ФЩЗуёЕВКЈ»ЈЁ2Ј©УЙ°ҙұИАэөД·ЦІгійСщҝЙөГ![]() өДЦө,ҝЙБРіцҙУ
өДЦө,ҝЙБРіцҙУ![]() БҫіөЦРЛж»ъСЎИЎБҪБҫөиөДЛщУРЗйҝц,ФЩХТіцЗЎУРТ»іөРРК»ЧЬАпіМі¬№э
БҫіөЦРЛж»ъСЎИЎБҪБҫөиөДЛщУРЗйҝц,ФЩХТіцЗЎУРТ»іөРРК»ЧЬАпіМі¬№э![]() Нт№«АпөДЗйҝц,АыУГ№ЕөдёЕРНҝЙөГҪб№ы.
Нт№«АпөДЗйҝц,АыУГ№ЕөдёЕРНҝЙөГҪб№ы.
КФМвҪвОцЈә
ЈЁ1Ј©ҙУХв140БҫЖыіөЦРИОИЎТ»БҫЈ¬ФтёГіөРРК»ЧЬАпіМі¬№э10Нт№«АпөДёЕВКОӘ![]() Ј®
Ј®
ЈЁ2Ј©ўЩТАМвТв![]() Ј®
Ј®
ўЪ5БҫіөЦРТСРРК»ЧЬАпіМІ»і¬№э10Нт№«АпөДіөУР3БҫЈ¬јЗОӘ![]() Ј»5БҫіөЦРТСРРК»ЧЬАпіМі¬№э10Нт№«АпөДіөУР2БҫЈ¬јЗОӘ
Ј»5БҫіөЦРТСРРК»ЧЬАпіМі¬№э10Нт№«АпөДіөУР2БҫЈ¬јЗОӘ![]() Ј®
Ј®
Ў°ҙУ5БҫіөЦРЛж»ъСЎИЎБҪБҫіөЎұөДЛщУРСЎ·Ё№І10ЦЦЈә![]() Ј®
Ј®
Ў°ҙУ5БҫіөЦРЛж»ъСЎИЎБҪБҫіөЈ¬ЗЎУРТ»БҫіөРРК»АпіМі¬№э10Нт№«АпЎ°өДСЎ·Ё№І6ЦЦЈә![]() Ј®
Ј®
ФтСЎИЎБҪБҫіөЦРЗЎУРТ»БҫіөРРК»АпіМі¬№э10Нт№«АпөДёЕВК![]() Ј®
Ј®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©=AsinЈЁwx+ҰХЈ©ЈЁxЎКRЈ¬wЈҫ0Ј¬0ЈјҰХЈј ![]() Ј©өДІҝ·ЦНјПуИзНјЛщКҫЈ®
Ј©өДІҝ·ЦНјПуИзНјЛщКҫЈ® 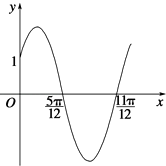
ЈЁ1Ј©ЗуәҜКэfЈЁxЈ©өДҪвОцКҪЈ»
ЈЁ2Ј©ЗуәҜКэgЈЁxЈ©=fЈЁx©Ғ ![]() Ј©©ҒfЈЁx+
Ј©©ҒfЈЁx+ ![]() Ј©өДөҘөчөЭФцЗшјдЈ®
Ј©өДөҘөчөЭФцЗшјдЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘөг![]() КЗ’ҒОпПЯ
КЗ’ҒОпПЯ![]() өДҪ№өг, Ифөг
өДҪ№өг, Ифөг![]() ФЪ
ФЪ![]() ЙП,ЗТ
ЙП,ЗТ![]() Ј®
Ј®
ЈЁ1Ј©Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ИфЦұПЯ![]() ҫӯ№эөг
ҫӯ№эөг![]() ЗТУл
ЗТУл![]() Ҫ»УЪ
Ҫ»УЪ![]() ЈЁТмУЪ
ЈЁТмУЪ![]() Ј©БҪөг, ЦӨГч: ЦұПЯ
Ј©БҪөг, ЦӨГч: ЦұПЯ![]() УлЦұПЯ
УлЦұПЯ![]() өДРұВКЦ®»эОӘіЈКэЈ®
өДРұВКЦ®»эОӘіЈКэЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() ЈЁ
ЈЁ![]() ОӘКөКэЈ¬
ОӘКөКэЈ¬ ![]() ОӘЧФИ»¶ФКэөДөЧКэЈ©Ј¬ЗъПЯ
ОӘЧФИ»¶ФКэөДөЧКэЈ©Ј¬ЗъПЯ![]() ФЪ
ФЪ![]() ҙҰөДЗРПЯУлЦұПЯ
ҙҰөДЗРПЯУлЦұПЯ![]() ЖҪРР.
ЖҪРР.
ЈЁ1Ј©ЗуКөКэ![]() өДЦөЈ¬ІўЕР¶ПәҜКэ
өДЦөЈ¬ІўЕР¶ПәҜКэ![]() ФЪЗшјд
ФЪЗшјд![]() ДЪөДБгөгёцКэЈ»
ДЪөДБгөгёцКэЈ»
ЈЁ2Ј©ЦӨГчЈәөұ![]() КұЈ¬
КұЈ¬ ![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР{an}өДЗ°nПоәНSn=3n+mЈЁmОӘіЈКэЈ¬nЎКN+Ј©
ЈЁ1Ј©Зуa1 Ј¬ a2 Ј¬ a3Ј»
ЈЁ2Ј©ИфКэБР{an}ОӘөИұИКэБРЈ¬ЗуіЈКэmөДЦөј°anЈ»
ЈЁ3Ј©¶ФУЪЈЁ2Ј©ЦРөДan Ј¬ јЗfЈЁnЈ©=ҰЛa2n+1©Ғ4ҰЛan+1©Ғ7Ј¬ИфfЈЁnЈ©Јј0¶ФИОТвөДХэХыКэnәгіЙБўЈ¬ЗуКөКэҰЛөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ФЪЛДАвЧ¶![]() ЦРЈ¬
ЦРЈ¬ ![]() ЖҪГж
ЖҪГж![]() КЗ
КЗ![]() өДЦРөгЈ¬
өДЦРөгЈ¬ ![]() КЗ
КЗ![]() ЙПөДөгЗТ
ЙПөДөгЗТ![]() ОӘ
ОӘ![]() ұЯ
ұЯ![]() ЙПөДёЯ.
ЙПөДёЯ.

ЈЁ1Ј©ЦӨГчЈә ![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() Ј¬ЗуИэАвЧ¶
Ј¬ЗуИэАвЧ¶![]() өДМе»эЈ»
өДМе»эЈ»
ЈЁ3Ј©ФЪПЯ¶О![]() ЙПКЗ·сҙжФЪХвСщТ»өг
ЙПКЗ·сҙжФЪХвСщТ»өг![]() Ј¬К№өГ
Ј¬К№өГ![]() ЖҪГж
ЖҪГж![]() ?ИфҙжФЪЈ¬Лөіц
?ИфҙжФЪЈ¬Лөіц![]() өгөДО»ЦГ.
өгөДО»ЦГ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪХэЛДАвЧ¶![]() ЦРЈ¬
ЦРЈ¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() ·ЦұрОӘ
·ЦұрОӘ![]() Ј¬
Ј¬ ![]() өДЦРөгЈ®
өДЦРөгЈ®
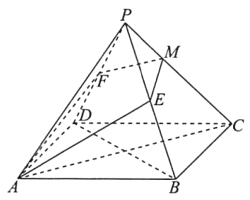
ЈЁўсЈ©ЗуЦӨЈә ![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁўтЈ©ЗуТмГжЦұПЯ![]() Ул
Ул![]() ЛщіЙҪЗөДУаПТЦөЈ»
ЛщіЙҪЗөДУаПТЦөЈ»
ЈЁўуЈ©ИфЖҪГж![]() УлАв
УлАв![]() Ҫ»УЪөг
Ҫ»УЪөг![]() Ј¬Зу
Ј¬Зу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
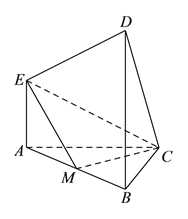
ЎҫМвДҝЎҝФЪИзНјЛщКҫөД¶аГжМеЦРЈ¬ ![]() ЖҪГж
ЖҪГж![]() Ј¬
Ј¬ ![]() ЖҪГж
ЖҪГж![]() Ј¬
Ј¬ ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬
Ј¬ ![]() КЗ
КЗ![]() өДЦРөгЈ®
өДЦРөгЈ®
ЈЁўсЈ©ЗуЦӨЈә ![]() Ј®
Ј®
ЈЁўтЈ©ЗуЖҪГж![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙөДИс¶юГжҪЗөДУаПТЦөЈ®
ЛщіЙөДИс¶юГжҪЗөДУаПТЦөЈ®
ЈЁўуЈ©ФЪАв![]() ЙПКЗ·сҙжФЪТ»өг
ЙПКЗ·сҙжФЪТ»өг![]() Ј¬К№өГЦұПЯ
Ј¬К№өГЦұПЯ![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙөДҪЗКЗ
ЛщіЙөДҪЗКЗ![]() Ј®ИфҙжФЪЈ¬Цёіцөг
Ј®ИфҙжФЪЈ¬Цёіцөг![]() өДО»ЦГЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
өДО»ЦГЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ
ФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ТФЧшұкФӯөг
ЦРЈ¬ТФЧшұкФӯөг![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬ ![]() ЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ТСЦӘЗъПЯ
ЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ТСЦӘЗъПЯ![]() өДј«Чшұк·ҪіМОӘЈә
өДј«Чшұк·ҪіМОӘЈә ![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() өДІОКэ·ҪіМКЗ
өДІОКэ·ҪіМКЗ![]() ЈЁ
ЈЁ![]() ОӘІОКэЈ¬
ОӘІОКэЈ¬ ![]() Ј©Ј®
Ј©Ј®
ЈЁ1Ј©ЗуЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©ЙиЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() Ҫ»УЪБҪөг
Ҫ»УЪБҪөг![]() Ј¬ЗТПЯ¶О
Ј¬ЗТПЯ¶О![]() өДЦРөгОӘ
өДЦРөгОӘ![]() Ј¬Зу
Ј¬Зу![]() Ј®
Ј®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com