
【题目】已知函数![]() (
(![]() 为实数,
为实数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求实数![]() 的值,并判断函数
的值,并判断函数![]() 在区间
在区间![]() 内的零点个数;
内的零点个数;
(2)证明:当![]() 时,
时, ![]() .
.
【答案】(1)![]() ,没有零点;(2)见解析.
,没有零点;(2)见解析.
【解析】【试题分析】(1)先借助导数的几何意义建立方程求出的值,再运用导数与函数的单调性之间的关系分析求解;(2)借助题设先将不等式进行等价转化,再运用导数知识进行分析推证:
(1)![]() ,由题设,可知曲线
,由题设,可知曲线![]() 在
在![]() 处的切线的斜率
处的切线的斜率![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() ,
,
∴![]() 在区间
在区间![]() 内为增函数,
内为增函数,
又![]() ,∴
,∴![]() 在区间
在区间![]() 内没有零点.
内没有零点.
(2)当![]() 时,
时, ![]() 等价于
等价于![]() ,记
,记![]() ,
,
则![]() ,当
,当![]() 时,
时, ![]() ,
,
∴当![]() 时,
时, ![]() 在区间
在区间![]() 内单调递增,
内单调递增,
∴![]() ,即
,即![]() ,两边取自然对数,得
,两边取自然对数,得![]() (
(![]() ),
),
∴要证明![]() (
(![]() ),只需证明
),只需证明![]() (
(![]() ),
),
即证当![]() 时,
时, ![]() ,①
,①
设![]() ,则
,则![]() ,令
,令![]() ,
,
则![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,又
内单调递增,又![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,∴存在
,∴存在![]() ,使得
,使得![]() ,
,
∴当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,∴
,∴![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增,
又![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时,取等号,即①式成立,
时,取等号,即①式成立,
∴![]() .
.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 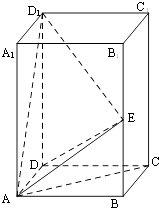
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,公比q≠1,等差数列{bn}满足b1=a1=3,b4=a2 , b13=a3 .
(1)求数列{an}与{bn}的通项公式;
(2)记cn=(﹣1)nbn+an , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高中入学新生的身高情况,从高一年级学生中按分层抽样共抽取了50名学生的身高数据,分组统计后得到了这50名学生身高的频数分布表:

(Ⅰ)在答题卡上作出这50名学生身高的频率分布直方图;
(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从身高在![]() 这6名学生中随机抽取3名,求至少抽到1名女生的概率.
这6名学生中随机抽取3名,求至少抽到1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com