
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
【答案】①③
【解析】解:①由正切函数的图象可知函数y=tanx在第一象限是增函数,命题正确;
②f(x)=cos2( ![]() ﹣x)=cos(
﹣x)=cos( ![]() ﹣2x)=sin2x,f(﹣x)=sin(﹣2x)=﹣sin2x=﹣f(x),故命题不正确;
﹣2x)=sin2x,f(﹣x)=sin(﹣2x)=﹣sin2x=﹣f(x),故命题不正确;
③∵0=4sin(2× ![]() ﹣
﹣ ![]() ),∴命题正确;
),∴命题正确;
④由2k ![]() ≤x+
≤x+ ![]() ≤2k
≤2k ![]() 可解得函数y=sin(x+
可解得函数y=sin(x+ ![]() )的单调递增区间为[2k
)的单调递增区间为[2k ![]() ,2k
,2k ![]() ]k∈Z,故命题不正确.
]k∈Z,故命题不正确.
综上,所有正确的命题的题号:①③,
故答案为:①③
①由正切函数的图象可知命题正确;
②化简可得f(x)=sin2x,由f(﹣x)=sin(﹣2x)=﹣sin2x=﹣f(x),可知命题不正确;
③代入有0=4sin(2× ![]() ﹣
﹣ ![]() ),可得命题正确;
),可得命题正确;
④由2k ![]() ≤x+
≤x+ ![]() ≤2k
≤2k ![]() 可解得函数y=sin(x+
可解得函数y=sin(x+ ![]() )的单调递增区间为[2k
)的单调递增区间为[2k ![]() ,2k
,2k ![]() ]k∈Z,比较即可得命题不正确.
]k∈Z,比较即可得命题不正确.


科目:高中数学 来源: 题型:
【题目】如图,为了测量正在海面匀速行驶的某船的速度,在海岸上选取距离1千米的两个观察
点C、D,在某天10:00观察到该船在A处,此时测得∠ADC=30°,2分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,
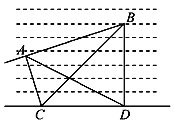
求该船航行的速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 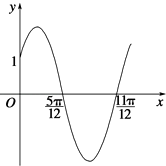
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间.
)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
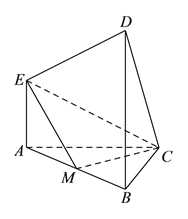
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com