
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
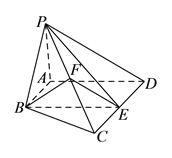
求证:(I)![]() 底面
底面![]() .
.
(II)平面![]() 平面
平面![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)直接根据面面垂直性质定理得线面垂直(2)先根据线面垂直性质定理得![]() ,而由三角形中位线性质得
,而由三角形中位线性质得![]() ,所以
,所以![]() ,再利用平几知识得
,再利用平几知识得![]() ,根据线面垂直判定定理得线面垂直,最后再根据面面垂直判定定理得结论
,根据线面垂直判定定理得线面垂直,最后再根据面面垂直判定定理得结论
试题解析:(I)证明:∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 底面
底面![]() .
.
(II)证明:∵![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
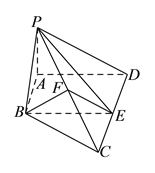
∴![]() ,
,
∴![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() ,
,
由(![]() )知,
)知,![]() 底面
底面![]() ,
,
∴![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】近几年电子商务蓬勃发展,在2017年的“年货节”期间,一网络购物平台推销了![]() 三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了
三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了![]() 三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对
三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对![]() 三种商品的抢购成功的概率分别为
三种商品的抢购成功的概率分别为![]() ,已知三件商品都被抢购成功的概率为
,已知三件商品都被抢购成功的概率为![]() ,至少有一件商品被抢购成功的概率为
,至少有一件商品被抢购成功的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若购物平台准备对抢购成功的![]() 三件商品进行优惠减免活动,
三件商品进行优惠减免活动, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,
百元, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,
百元, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,求该名网购者获得减免的总金额(单位:百元)的分布列和数学期望.
百元,求该名网购者获得减免的总金额(单位:百元)的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一期间,某商场决定从![]() 种服装、
种服装、![]() 种家电、
种家电、![]() 种日用品中,选出
种日用品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出![]() 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高![]() 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有![]() 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为![]() 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为![]() 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为 ![]() 元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是![]() ,请问: 商场将奖金数额
,请问: 商场将奖金数额![]() 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
![]()
(1)画出茎叶图
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是 ![]() ,则sin2θ﹣cos2θ的值等于( )
,则sin2θ﹣cos2θ的值等于( ) 
A.1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(
=( ![]() sinx,m+cosx),
sinx,m+cosx), ![]() =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= ![]()
(1)求函数f(x)的解析式;
(2)当x∈[﹣ ![]() ,
, ![]() ]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com