
【题目】如图所示, ![]() 矩形
矩形![]() 所在的平面,
所在的平面, ![]() 分别是
分别是![]() 的中点.
的中点.
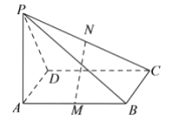
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() .
.
(3)当![]() 满足什么条件时,能使
满足什么条件时,能使![]() 平面
平面![]() 成立?并证明你的结论.
成立?并证明你的结论.
【答案】(1)见解析;(2)见解析;(3)当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立.证明见解析。
成立.证明见解析。
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,证明四边形
,证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,利用线面平行的判定,即可得出结论;(2)由线面垂直得
,利用线面平行的判定,即可得出结论;(2)由线面垂直得![]() ,由矩形性质得
,由矩形性质得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,由此能证明
,由此能证明![]() ;(3)当
;(3)当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立,可利用等腰三角形的性质以及线面垂直的判定定理证明.
成立,可利用等腰三角形的性质以及线面垂直的判定定理证明.
试题解析:( ![]() )证明:取
)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .
.
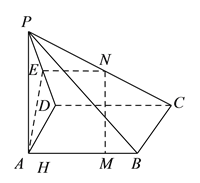
∵![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
又∵![]() ,
, ![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )∵
)∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]()
∴![]() .
.
(![]() )当
)当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立,
成立,
现证明如下:
∵![]() ,
, ![]() 是
是![]() 中点,
中点,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
由(![]() )可知
)可知![]() ,
,
∴![]() 平面
平面![]() .
.
故当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立.
成立.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面垂直的性质定理与判定定理,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最小正周期是
)的最小正周期是 ![]() ,最小值是﹣2,且图象经过点(
,最小值是﹣2,且图象经过点( ![]() ,0),则f(0)= .
,0),则f(0)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为了测量正在海面匀速行驶的某船的速度,在海岸上选取距离1千米的两个观察
点C、D,在某天10:00观察到该船在A处,此时测得∠ADC=30°,2分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,
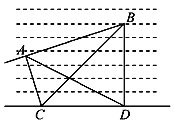
求该船航行的速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD= ![]() AA1=2.
AA1=2. 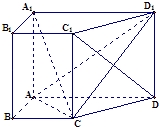
(1)求证:直线C1D⊥平面ACD1;
(2)试求三棱锥A1﹣ACD1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 有两个极值点
有两个极值点![]() 且
且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 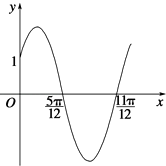
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间.
)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com