
【题目】已知ABCD为矩形,AB=3,BC=2,在矩形ABCD内随机取一点P,点P到矩形四个顶点的距离都大于1的概率为 .
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 上关于原点
上关于原点![]() 对称的任意两点,且点
对称的任意两点,且点![]() 都不在
都不在![]() 轴上.
轴上.
(1)若![]() ,求证: 直线
,求证: 直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)若椭圆长轴长为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,设
上,设![]() 是椭圆上异于点
是椭圆上异于点![]() 的任意两点,且
的任意两点,且![]() .问直线
.问直线![]() 是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角三角形中,边a、b是方程x2﹣2 ![]() x+2=0的两根,角A、B满足:2sin(A+B)﹣
x+2=0的两根,角A、B满足:2sin(A+B)﹣ ![]() =0,求角C的度数,边c的长度及△ABC的面积.
=0,求角C的度数,边c的长度及△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2.若数列{bn}满足bn=10﹣log2an , 则是数列{bn}的前n项和取最大值时n的值为( )
A.8
B.10
C.8或9
D.9或10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.数据分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.
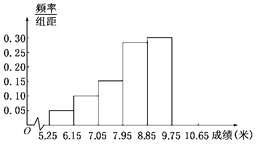
(I)求这次铅球测试成绩合格的人数;
(II)若参加测试的学生中9人成绩优秀,现要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知学生![]() 、
、![]() 的成绩均为优秀,求两人
的成绩均为优秀,求两人![]() 、
、![]() 至少有1人入选的概率.
至少有1人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AB⊥DA,CE= ![]() ,∠ADC=
,∠ADC= ![]() ;E为AD边上一点,DE=1,EA=2,∠BEC=
;E为AD边上一点,DE=1,EA=2,∠BEC= ![]()
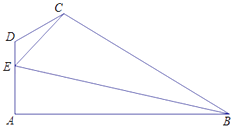
(1)求sin∠CED的值;
(2)求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com