
分析 (1)设正四面体为A-BCD,过D作DE⊥BC,交BC于E,作AH⊥底面BCD于点H,交DE于H,先求出DH,由此能求出正四面体的高AH.
(2)设正四面体内切球的球心为O,半径为r,O点与A、B、C、D相连得四个小三棱锥,设原三棱锥的底面积为S,则每个侧面积均为S,由此能求出结果.
解答 解:(1)设正四面体为A-BCD,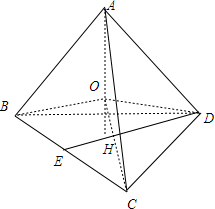
过D作DE⊥BC,交BC于E,
作AH⊥底面BCD于点H,交DE于H,
则DE=$\sqrt{{a}^{2}-(\frac{a}{2})^{2}}$=$\frac{\sqrt{3}}{2}a$,DH=$\frac{2}{3}DE=\frac{2}{3}×\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{3}a$,
∴AH=$\sqrt{{a}^{2}-(\frac{\sqrt{3}}{3}a)^{2}}$=$\frac{\sqrt{6}}{3}a$.
∴正四面体的高为$\frac{\sqrt{6}}{3}a$.
(2)设正四面体内切球的球心为O,半径为r,
O点与A、B、C、D相连得四个小三棱锥,
设原三棱锥的底面积为S,则每个侧面积均为S,
∴4×$\frac{1}{3}Sr$=$\frac{1}{3}S×AH$,
∴r=$\frac{1}{4}AH=\frac{\sqrt{6}}{12}a$,
∴正四面体内切球的体积V=$\frac{4}{3}π{r}^{3}$=$\frac{\sqrt{6}}{216}π{a}^{3}$.
点评 本题考查正四面体的高、正四面体内切球的半径和体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
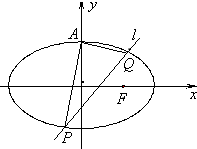 如图,已知椭圆$C:\frac{x^2}{a^2}+{y^2}=1(a>1)$的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
如图,已知椭圆$C:\frac{x^2}{a^2}+{y^2}=1(a>1)$的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com