
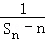 ,若C1+C2+C3+…+Cn≥m2﹣
,若C1+C2+C3+…+Cn≥m2﹣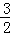 对任意正整数n恒成立,求实数m 的取值范围.
对任意正整数n恒成立,求实数m 的取值范围.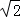 ,
,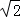 ]
]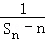 =
=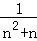 =
=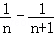 ,从而利用裂项求和的方法求出C1+C2+C3+…+Cn=1﹣
,从而利用裂项求和的方法求出C1+C2+C3+…+Cn=1﹣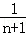 ,得到当n=1时它的最小值为
,得到当n=1时它的最小值为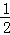 .因此原不等式恒成立,即
.因此原不等式恒成立,即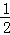 ≥m2﹣
≥m2﹣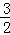 ,解之得﹣
,解之得﹣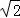 ≤m≤
≤m≤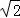 ,可得实数m的取值范围.
,可得实数m的取值范围.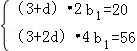 ,解之得b1=d=2
,解之得b1=d=2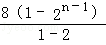 ﹣(2n+1)2n+1=﹣2+(1﹣2n)2n+1,
﹣(2n+1)2n+1=﹣2+(1﹣2n)2n+1,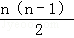 ×2=n2+2n
×2=n2+2n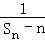 =
=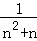 =
=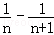
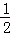 )+(
)+(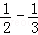 )+…+(
)+…+(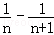 )=1﹣
)=1﹣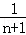
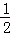
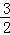 对任意正整数n恒成立,
对任意正整数n恒成立, ≥m2﹣
≥m2﹣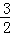 ,解之得﹣
,解之得﹣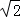 ≤m≤
≤m≤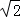 ,即实数m的取值范围是[﹣
,即实数m的取值范围是[﹣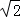 ,
,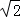 ].
].

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com