
【题目】一个小商店从一家食品有限公司购进10袋白糖,每袋白糖的标准重量是500g,为了了解这些白糖的实际重量,称量出各袋白糖的实际重量(单位:g)如下:503,502,496,499,491,498,506,504,501,510
(1)求这10袋白糖的平均重量![]() 和标准差s;
和标准差s;
(2)从这10袋中任取2袋白糖,那么其中恰有一袋的重量不在(![]() s,
s,![]() s)的概率是多少?(附:
s)的概率是多少?(附:![]() 5.08,
5.08,![]() 16.06,
16.06,![]() 5.09,
5.09,![]() 16.09)
16.09)
【答案】(1)501,5.08;(2)![]() .
.
【解析】
(1)根据提供的数据,利用平均数和方差公式求解.
(2)根据(1)的结合,算出重量在(![]() s,
s,![]() s)内的袋数和不在内的袋数,然后得出从10袋中选2袋的方法数和恰有一袋的方法数,再利用古典概型的概率公式求解.
s)内的袋数和不在内的袋数,然后得出从10袋中选2袋的方法数和恰有一袋的方法数,再利用古典概型的概率公式求解.
(1)根据题意,10袋白糖的实际重量如下:503,502,496,499,491,498,506,504,501,510,
则其平均重量![]() (503+502+496+499+491+498+506+504+501+510)=500
(503+502+496+499+491+498+506+504+501+510)=500![]() (3+2﹣4﹣1﹣9﹣2+6+4+1+10)=501,
(3+2﹣4﹣1﹣9﹣2+6+4+1+10)=501,
其方差S2![]() [(503﹣501)2+(502﹣501)2+(496﹣501)2+(499﹣501)2+(491﹣501)2+(498﹣501)2+(506﹣501)2+(504﹣501)2+(501﹣501)2+(510﹣501)2]=25.8;
[(503﹣501)2+(502﹣501)2+(496﹣501)2+(499﹣501)2+(491﹣501)2+(498﹣501)2+(506﹣501)2+(504﹣501)2+(501﹣501)2+(510﹣501)2]=25.8;
则其标准差s![]() 5.08;
5.08;
(2)根据题意,由(1)的结论,10袋白糖在(![]() s,
s,![]() s)之间的有503,502,496,499,498,506,504,501,共8袋,
s)之间的有503,502,496,499,498,506,504,501,共8袋,
从10袋白糖中任取两袋,有C102=45种取法,
其中恰有一袋的重量不在(![]() s,
s,![]() s)的情况有8×2=16种,
s)的情况有8×2=16种,
则恰有一袋的重量不在(![]() s,
s,![]() s)的概率P
s)的概率P![]() .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC﹣A1B1C1中,点O、E分别是A1C1、A1B1的中点,A1C与AC1交于点F,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
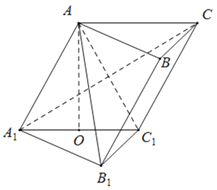
(1)求证:EF∥平面BB1C1C;
(2)求A1C1与平面AA1B1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为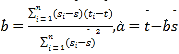 ,(说明:
,(说明:![]() 的导函数为
的导函数为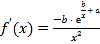 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]()
![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,曲线
轴的正半轴建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).
为参数).
(1)请写出直线![]() 的参数方程;
的参数方程;
(2)求直线![]() 与曲线
与曲线![]() 交点
交点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为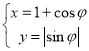 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值与最小值.
的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左顶点为A,离心率为
)的左顶点为A,离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)若直线![]() (
(![]() )与椭圆C交于E,F两点,直线
)与椭圆C交于E,F两点,直线![]() ,
,![]() 分别与y轴交于点M,N,求证:在x轴上存在点P,使得无论非零实数k怎样变化,以
分别与y轴交于点M,N,求证:在x轴上存在点P,使得无论非零实数k怎样变化,以![]() 为直径的圆都必过点P,并求出点P的坐标.
为直径的圆都必过点P,并求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com