
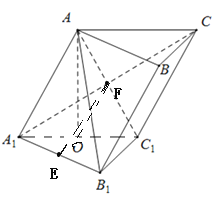
【题目】如图,在斜三棱柱ABC﹣A1B1C1中,点O、E分别是A1C1、A1B1的中点,A1C与AC1交于点F,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
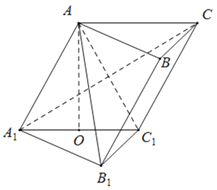
(1)求证:EF∥平面BB1C1C;
(2)求A1C1与平面AA1B1所成角的正弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)推导出OE∥B1C1,OF∥C1C,,从而平面OEF∥平面BB1C1C,由此能证明EF∥平面BB1C1C;
(2)设点C1到平面AA1B1的距离为d,由![]() ,求出
,求出![]() 由此能求出A1C1与平面AA1B1所成角的正弦值.
由此能求出A1C1与平面AA1B1所成角的正弦值.
证明:(1)∵O,E分别是A1C1、A1B1的中点,A1C与AC1交于点F,
∴OE![]() B1C1,OF
B1C1,OF![]() C1C,
C1C,
又![]() 平面BB1C1C,
平面BB1C1C,![]() 平面BB1C1C,
平面BB1C1C,
![]() 平面BB1C1C,
平面BB1C1C,
同理![]() 平面BB1C1C,
平面BB1C1C,
又![]() ,
,![]() 平面OEF,
平面OEF,
∴平面OEF![]() 平面BB1C1C,
平面BB1C1C,
∵EF平面OEF,
∴EF![]() 平面BB1C1C.
平面BB1C1C.
(2)设点C1到平面AA1B1的距离为d,
∵![]() ,
,
∴![]() ,
,
AO![]() ,OB1
,OB1![]() ,
,
AB1![]() 2
2![]() ,
,
∵△AA1B1中,A1B1=AB1=2![]() ,AA=2,
,AA=2,
边AA上的高为:![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得d![]() ,
,
设A1C1与平面AA1B1所成角为θ,
∴A1C1与平面AA1B1所成角的正弦值为:
sinθ![]() .
.


科目:高中数学 来源: 题型:
【题目】斐波那契数列(![]() )又称黄金分割数列,因数学家列昂纳多斐波那契(
)又称黄金分割数列,因数学家列昂纳多斐波那契(![]() )以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列
)以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35.
地区当中“非常满意”的观众的概率为0.35.
非常满意 | 满意 | 合计 | |
| 30 | 15 | |
|
|
| |
合计 |
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若直线![]() 且曲线
且曲线![]() 在A处的切线与
在A处的切线与![]() 在B处的切线相互平行,求a的取值范围;
在B处的切线相互平行,求a的取值范围;
(Ⅱ)设![]() 在其定义域内有两个不同的极值点
在其定义域内有两个不同的极值点![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个小商店从一家食品有限公司购进10袋白糖,每袋白糖的标准重量是500g,为了了解这些白糖的实际重量,称量出各袋白糖的实际重量(单位:g)如下:503,502,496,499,491,498,506,504,501,510
(1)求这10袋白糖的平均重量![]() 和标准差s;
和标准差s;
(2)从这10袋中任取2袋白糖,那么其中恰有一袋的重量不在(![]() s,
s,![]() s)的概率是多少?(附:
s)的概率是多少?(附:![]() 5.08,
5.08,![]() 16.06,
16.06,![]() 5.09,
5.09,![]() 16.09)
16.09)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴上的椭圆E经过点![]() ,且焦距为
,且焦距为![]() .
.
(1)求椭圆E的标准方程;
(2)直线![]() 与椭圆E交于不同的两点A、B,线段AB的垂直平分线交y轴于点M,若
与椭圆E交于不同的两点A、B,线段AB的垂直平分线交y轴于点M,若![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com