练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f(x)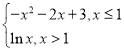＝,若关于x的方程f(x)＝kx－恰有4个不相等的实数根，则实数k的取值范围是(　　)

    A. B.

    C. D.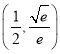

    【答案】D

    【解析】

    由已知可将问题转化为：y＝f(x)的图象和直线y＝kx－有4个交点，作出图象，由图可得：点(1,0)必须在直线y＝kx－的下方，即可求得：k＞；再求得直线y＝kx－和y＝ln x相切时，k＝；结合图象即可得解.

    若关于x的方程f(x)＝kx－恰有4个不相等的实数根，

    则y＝f(x)的图象和直线y＝kx－有4个交点．作出函数y＝f(x)的图象，如图，

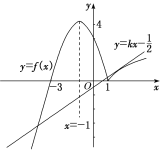
    故点(1,0)在直线y＝kx－的下方．

    ∴k×1－＞0，解得k＞.

    当直线y＝kx－和y＝ln x相切时，设切点横坐标为m，

    则k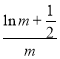＝＝，∴m＝.

    此时，k＝＝，f(x)的图象和直线y＝kx－有3个交点，不满足条件，

    故所求k的取值范围是，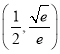

    故选D..

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在斜三棱柱ABC﹣A1B1C1中，点O、E分别是A1C1、A1B1的中点，A1C与AC1交于点F，AO⊥平面A1B1C1．已知∠BCA＝90°，AA1＝AC＝BC＝2．

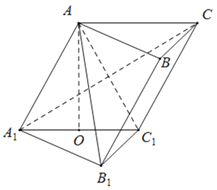
    （1）求证：EF∥平面BB1C1C；

    （2）求A1C1与平面AA1B1所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为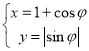（为参数）.在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，直线的极坐标方程为.

    （1）求曲线的普通方程及直线的直角坐标方程；

    （2）求曲线上的点到直线的距离的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年11月15日，我市召开全市创建全国文明城市动员大会，会议向全市人民发出动员令，吹响了集结号.为了了解哪些人更关注此活动，某机构随机抽取了年龄在15～75岁之间的100人进行调查，并按年龄绘制的频率分布直方图如图所示，其分组区间为：，，，，，.把年龄落在和内的人分别称为“青少年人”和“中老年人”，经统计“青少年人”与“中老年人”的人数之比为.

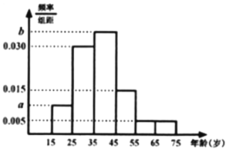
    （1）求图中的值，若以每个小区间的中点值代替该区间的平均值，估计这100人年龄的平均值；

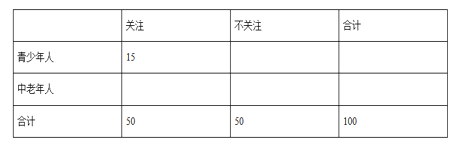
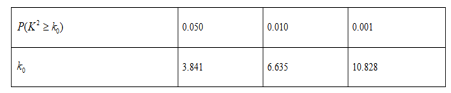
    （2）若“青少年人”中有15人关注此活动，根据已知条件完成题中的列联表，根据此统计结果，问能否有的把握认为“中老年人”比“青少年人”更加关注此活动？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.

    表1：甲套设备的样本的频数分布表

    质量指标值

    [95,100)

    [100,105)

    [105,110)

    [110,115)

    [115,120)

    [120,125]

    频数

    1

    4

    19

    20

    5

    1

    图1：乙套设备的样本的频率分布直方图

    （1）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；

    甲套设备

    乙套设备

    合计

    合格品

    不合格品

    合计

    		，求的期望.

    附：

    P(K2≥k0)

    0.15

    0.10

    0.050

    0.025

    0.010

    k0

    2.072

    2.706

    3.841

    5.024

    6.635

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市为了节约生活用水，计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准：用水量不超过a的部分按照平价收费，超过a的部分按照议价收费)．为了较为合理地确定出这个标准，通过抽样获得了40位居民某年的月均用水量(单位：吨)，按照分组制作了频率分布直方图，

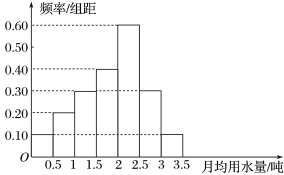
    （Ⅰ）用该样本估计总体：

    （1）估计该市居民月均用水量的平均数；

    （2）如果希望86%的居民每月的用水量不超出标准，则月均用水量a的最低标准定为多少吨？

    （Ⅱ）在该样本中月均用水量少于1吨的居民中随机抽取两人，其中两人月均用水量都不低于0.5吨的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C:（）的左顶点为A，离心率为，点在椭圆C上.

    （1）求椭圆C的方程；

    （2）若直线（）与椭圆C交于E，F两点，直线，分别与y轴交于点M，N，求证:在x轴上存在点P，使得无论非零实数k怎样变化，以为直径的圆都必过点P，并求出点P的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据气象部门预报，在距离某个码头A南偏东45°方向的600km处的热带风暴中心B正以30km/h的速度向正北方向移动，距离风暴中心450km以内的地区都将受到影响，从现在起经过___小时后该码头A将受到热带风暴的影响（精确到0.01）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆经过两点，为坐标原点.

    （1）求椭圆的标准方程；

    （2）设动直线与椭圆有且仅有一个公共点，且与圆相交于两点，试问直线与的斜率之积是否为定值？若是，求出该定值；若不是，说明理由.

    查看答案和解析>>

    同步练习册答案