练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，三棱柱中， 是正三角形，四边形是矩形，且.

    （1）求证:平面平面；

    （2）若点在线段上，且，当三棱锥的体积为时，求实数的值.

    【答案】（1）见解析（2）

    【解析】试题分析：（1）先根据计算，利用勾股定理得，再根据矩形性质得，利用线面垂直判定定理得平面，最后根据面面垂直判定定理得平面 平面.（2）由等体积法得，因此 ，从而问题转化为求，而由平面 平面，结合面面垂直性质定理可得上高为平面的垂线，最后在三角形求出高及底面面积可得锥的体积，进而可得实数的值.

    试题解析：（1）依题意可得，∴, ,又四边形是矩形，

    ∴.

    又∵平面, 平面, ,

    ∴平面,而平面,

    ∴平面 平面.

    （2）依题意可得,取中点,所以，且，又由（1)知平面 平面，则平面.

    如图，过点作交于点，则平面,

    的面积为，

    .

    由得 .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    (1)若曲线在处的切线平行于直线，求a的值；

    (2)讨论函数的单调性；

    (3) 若，且对时，恒成立，求实数的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】方程 在（0，2π）内有相异两解α，β，则α+β=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中， 平面，底面为矩形， ，该四棱锥的外接球的体积为，则到平面的距离为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为实数)的图像在点处的切线方程为.

    （1）求实数的值及函数的单调区间；

    （2）设函数，证明时， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）试确定的取值范围，使得函数在上为单调函数；

    （2）若为自然数，则当取哪些值时，方程在上有三个不相等的实数根，并求出相应的实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

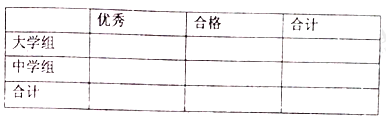
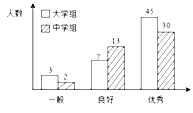
    【题目】传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随即从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图.

    （Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？

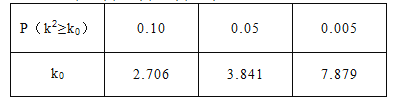
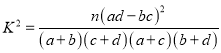    注：其中.

    （Ⅱ）在优秀等级的选手中取6名，依次编号为1,2,3,4,5,6，在良好等级的选手中取6名，依次编号为1,2,3,4,5,6，在选出的6名优秀等级的选手中任取一名，记其编号为，在选出的6名良好等级的选手中任取一名，记其编号为，求使得方程组有唯一一组实数解的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： （a＞b＞0）的焦距为，且椭圆C过点A（1， ），

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）若O是坐标原点，不经过原点的直线L：y=kx+m与椭圆交于两不同点P（x1，y1），Q（x2，y2），且y1y2=k2x1x2，求直线L的斜率k；

    （Ⅲ）在（Ⅱ）的条件下，求△OPQ面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（14分）一根直木棍长为6m，现将其锯为2段．

    （1）若两段木棍的长度均为正整数，求恰有一段长度为2m的概率；

    （2）求锯成的两段木棍的长度均大于2m的概率．

    查看答案和解析>>

    同步练习册答案