练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数

    (1)若曲线在处的切线平行于直线，求a的值；

    (2)讨论函数的单调性；

    (3) 若，且对时，恒成立，求实数的取值范围

    【答案】(1) (2) 当时，在递增；当时，在递减，在递增； (3)

    【解析】试题分析：（1）根据曲线在处的切线平行于直线，则，得出a值；（2）对函数求导，讨论，两种情况得单调性（3）对时，恒成立可选择变量分离，构造新函数研究最值，得结果.

    试题解析：

    (1) 定义域为

    直线的斜率为,


    (2)定义域为，，若，则在递增；

    若，令得；令得；

    综上得：当时，在递增；当时，在递减，在递增；

    (3) ，且对时，恒成立

    . 即

    设

    ，

    当时, ,为增函数

    当时, ,为减函数

    所以当时,函数在上取到最大值,且

    所以 所以

    所以实数的取值范围为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点，求：

    （Ⅰ）过点与原点距离为2的直线的方程；

    （Ⅱ）过点与原点距离最大的直线的方程，最大距离是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学组织了一次高二文科学生数学学业水平模拟测试，学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析，分别制成了如图所示的男生和女生数学成绩的频率分布直方图．

    （Ⅰ）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？

    （Ⅱ）在（Ⅰ）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意任取2人，求至少有一名男生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， = .

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若函数有两个零点.

    (1)求满足条件的最小正整数的值；

    (2)求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在某港口处获悉,其正东方向距离20n mile的处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°距港口10n mile的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.

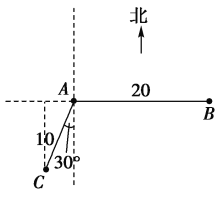
    （1）求接到救援命令时救援船距渔船的距离;

    （2）试问救援船在C处应朝北偏东多少度的方向沿直线前往B处救援?（已知）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用1、2、3、4、5、6这六个数字可组成多少个无重复数字且不能被5整除的五位数？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，（其中为在点处的导数， 为常数).

    （1）求的值；

    （2）求函数的单调区间；

    （3）设函数，若函数在区间上单调递增，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （Ⅰ）证明： ，直线都不是曲线的切线；

    （Ⅱ）若，使成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中， 是正三角形，四边形是矩形，且.

    （1）求证:平面平面；

    （2）若点在线段上，且，当三棱锥的体积为时，求实数的值.

    查看答案和解析>>

    同步练习册答案