
| A. | $y=±\frac{3}{4}x$ | B. | $y=±\frac{4}{3}x$ | C. | $y=±\frac{{\sqrt{6}}}{3}x$ | D. | $y=±\frac{{\sqrt{6}}}{2}x$ |
分析 利用双曲线的离心率,而渐近线中a,b关系,结合c2=a2+b2找关系即可.
解答 解:e=$\frac{c}{a}$=$\frac{5}{3}$,又因为在双曲线中,c2=a2+b2,
所以e2=$\frac{{c}^{2}}{{a}^{2}}$=1+$\frac{{b}^{2}}{{a}^{2}}$=$\frac{25}{9}$,
故$\frac{b}{a}$=$\frac{4}{3}$,
所以双曲线C:$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1的渐近线方程为y=$±\frac{a}{b}$x=$±\frac{3}{4}$x
故选:A.
点评 本题考查双曲线的性质:离心率和渐近线,属基础知识的考查.在双曲线中,要注意条件c2=a2+b2的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
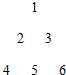 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2015,则i、j的值分别为63,62.
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2015,则i、j的值分别为63,62.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ②④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com