
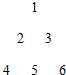 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2015,则i、j的值分别为63,62.
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2015,则i、j的值分别为63,62. 分析 第一行有一个数,第二行有两个数…,第n行有n个数字,这样每一行的数字个数组成一个等差数列,表示出等差数列的前项和,使得和大于或等于2009,解出不等式,求出n的值,得到结果.
解答 解:由题意可知,第一行有一个数,第二行有两个数,第三行有三个数,…,第62行有62个数,第63行有63个数,第n行有n个数字,这样每一行的数字个数组成一个等差数列,
∴前n项的和是$\frac{n(n+1)}{2}$,
∵当n=63时,$\frac{63×64}{2}$=2016>2009,n=62时,$\frac{62×63}{2}$=1053<2009,
∴第62行的最后一个数为1+2+3+…+62=1953,第63行第一个数为1954
∴2015为第63行,第62个数.
故答案为:63,62.
点评 本题的考点是归纳推理,主要考查数列的性质和应用,本题解题的关键是看出所形成的数列是一个等差数列,利用等差数列的前项和,使得和大于或等于2015求解.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,g(x)=$\frac{{x}^{2}}{x}$ | B. | f(x)=2x+1,g(x)=2x-1 | C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=1,g(x)=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高一 | 高二 | 合计 | |
| 合格人数 | 80 | m | 140 |
| 不合格人数 | n | 40 | 60 |
| 合计 | 100 | 100 | 200 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{3}{4}x$ | B. | $y=±\frac{4}{3}x$ | C. | $y=±\frac{{\sqrt{6}}}{3}x$ | D. | $y=±\frac{{\sqrt{6}}}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com