
���� ��1������κ���f��x��=ax2+bx��f'��x��=2ax+b����a=b=1��֪f��x��=x2+x���ɣ�n��Sn����y=x2+x�ϣ�֪Sn=n2+n���ɴ����������{an}��ͨ�ʽ��
��2����bn=$\frac{3}{{a}_{n}{a}_{n+1}}$=$\frac{3}{4}$��$\frac{1}{n}$-$\frac{1}{n+1}$����֪Tn=$\frac{3}{4}$��1-$\frac{1}{n+1}$����$\frac{m}{16}$��������ɴ����������n��N*��������m�ķ�Χ��
��� �⣺��1������������κ���Ϊy=ax2+bx
��f�䣨x��=2ax+b��
��f�䣨x��=2x+1��
��a=1��b=1��
��f��x��=x2+x��
�ߵ㣨n��Sn����n��N*�����ں���y=f��x����ͼ���ϣ�
��Sn=n2+n��
��n=1ʱ��Sn=a1=2��
��n��2ʱ��an=Sn-Sn-1=2n��
����a1=2����an=2n��
������{an}��ͨ�ʽΪan=2n��n��N*����
��2���ɣ�1����bn=$\frac{3}{{a}_{n}{a}_{n+1}}$=$\frac{3}{2n•2��n+1��}$=$\frac{3}{4}$��$\frac{1}{n}$-$\frac{1}{n+1}$����
��Tn=$\frac{3}{4}$[��1-$\frac{1}{2}$��+��$\frac{1}{2}$-$\frac{1}{3}$��+��+��$\frac{1}{n}$-$\frac{1}{n+1}$��]=$\frac{3}{4}$��1-$\frac{1}{n+1}$����
�Ѵ���ʽ$\frac{3}{4}$��1-$\frac{1}{n+1}$������n�ĺ����գ�n����
��ˣ�ʹ�æգ�x��=$\frac{3}{4}$��1-$\frac{1}{n+1}$����$\frac{m}{16}$�������m�������� �գ�n�������ֵ$\frac{m}{16}$��
�գ�x��max=[$\frac{3}{4}$��1-$\frac{1}{n+1}$��]max��$\frac{3}{4}$����$\frac{3}{4}$��$\frac{m}{16}$����m��12��
�ʣ�����Ҫ�����С����mΪ12��
���� ���⿼�������벻��ʽ���ۺϣ��ۺ���ǿ���ѶȽϴ��״����ǻ���֪ʶ���ι̣�������������֪ʶ���еȼ�ת��ת��������ʱҪ�������⣬ע���ھ������е�����������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
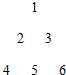 ������������С�´���С�Ҵ��ԭ���ų���ͼ������������ÿ�б���һ�ж�һ����������ai��j��i��j��N*����λ����������������д�����������i�С�������������j��������a4��2=8����ai��j=2015����i��j��ֵ�ֱ�Ϊ63��62��
������������С�´���С�Ҵ��ԭ���ų���ͼ������������ÿ�б���һ�ж�һ����������ai��j��i��j��N*����λ����������������д�����������i�С�������������j��������a4��2=8����ai��j=2015����i��j��ֵ�ֱ�Ϊ63��62���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{175}{264}$ | B�� | $\frac{11}{24}$ | C�� | $\frac{175}{132}$ | D�� | $\frac{2015}{2016}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com