
| A. | $\frac{175}{264}$ | B. | $\frac{11}{24}$ | C. | $\frac{175}{132}$ | D. | $\frac{2015}{2016}$ |
分析 f′(x)=2x+a,根据函数f(x)=x2+ax的图象在点A(0,f(0))处的切线l与直线2x-y+2=0平行,可得f′(0)=a=2,于是f(x)=x2+2x.得到数列$\left\{{\frac{1}{f(n)}}\right\}$的通项公式,利用“裂项求和”即可得出.
解答 解:f′(x)=2x+a,
∵函数f(x)=x2+ax的图象在点A(0,f(0))处的切线l与直线2x-y+2=0平行,
∴f′(0)=a=2,
∴f(x)=x2+2x.
∴$\frac{1}{f(n)}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴数列{$\frac{1}{f(n)}$}的前n项和为Sn=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{n-1}$-$\frac{1}{n+1}$)+($\frac{1}{n}$-$\frac{1}{n+2}$)]
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
则S10=$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{11}$-$\frac{1}{12}$)
=$\frac{175}{264}$.
故选:A.
点评 本题考查了导数的几何意义、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
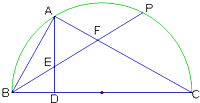 如图,在以BC为直径的半圆上任意取一点P,过$\widehat{BP}$的中点A作AD⊥BC于D,连接BP交AD于E,交AC于F,则EF:BE等于( )
如图,在以BC为直径的半圆上任意取一点P,过$\widehat{BP}$的中点A作AD⊥BC于D,连接BP交AD于E,交AC于F,则EF:BE等于( )| A. | 1:2 | B. | 1:1 | C. | 2:1 | D. | 2:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com