
分析 (1)化简得到ρ2=4ρcosθ+4ρsinθ,根据x2+y2=ρ2,x=ρcosθ,y=ρsinθ,替换即可;
(2)求出直线l的参数方程,代入圆的方程,结合t的几何意义求出答案即可.
解答 解:(1)由$ρ=4\sqrt{2}sin(\frac{3π}{4}-θ)$,可得ρ=4cosθ+4sinθ,…(2分)
∴ρ2=4ρcosθ+4ρsinθ,
∴x2+y2=4x+4y,
即(x-2)2+(y-2)2=8. …(5分)
(2)过点P(0,2)作斜率为$\sqrt{3}$的直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=2+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数) …(7分)
代入(x-2)2+(y-2)2=8,得t2-2t-4=0,
设点A、B对应的参数分别为t1、t2,则t1+t2=2,t1•t2=-4…(8分)
由t的几何意义可得$|{\frac{1}{|PA|}-\frac{1}{|PB|}}|=|{\frac{1}{{|{t_1}|}}-\frac{1}{{|{t_2}|}}}|=\frac{{|{|{t_1}|-|{t_2}|}|}}{{|{t_1}||{t_2}|}}=\frac{{|{t_1}+{t_2}|}}{{|{t_1}{t_2}|}}=\frac{1}{2}$. …(10分)
点评 本题考查了极坐标方程、参数方程问题,考查三角函数以及绝对值的意义,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{175}{264}$ | B. | $\frac{11}{24}$ | C. | $\frac{175}{132}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
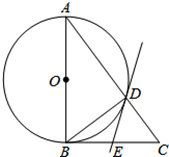 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com