
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 原式各项中的角度变形后,利用诱导公式及特殊角的三角函数值求出结果,即可做出判断.
解答 解:①sin(-660°)=sin(-720°+60°)=sin60°=$\frac{\sqrt{3}}{2}$>0;
②cos(-740°)=cos(-720°-20°)=cos20°>0;
③cos570°=cos(360°+210°)=cos210°=cos(180°+30°)=-cos30°=$-\frac{\sqrt{3}}{2}$<0;
④sin(-420°)=sin(-360-60°)=-sin60°<0,
则负值的个数是2.
故选:B.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.


科目:高中数学 来源: 题型:解答题
| 高一 | 高二 | 合计 | |
| 合格人数 | 80 | m | 140 |
| 不合格人数 | n | 40 | 60 |
| 合计 | 100 | 100 | 200 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
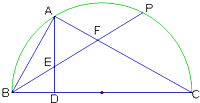 如图,在以BC为直径的半圆上任意取一点P,过$\widehat{BP}$的中点A作AD⊥BC于D,连接BP交AD于E,交AC于F,则EF:BE等于( )
如图,在以BC为直径的半圆上任意取一点P,过$\widehat{BP}$的中点A作AD⊥BC于D,连接BP交AD于E,交AC于F,则EF:BE等于( )| A. | 1:2 | B. | 1:1 | C. | 2:1 | D. | 2:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com