
分析 (Ⅰ)根据向量的垂直,得到$\overrightarrow{a}$•$\overrightarrow{b}$=0,求出tan2x的值即可;
(Ⅱ)求出f(x)的表达式,化简,从而求出函数的递增区间即可.
解答 解:(Ⅰ)由$\overrightarrow a⊥\overrightarrow b$,
得$\overrightarrow a•\overrightarrow b=2\sqrt{3}sinxcosx-cos2x=\sqrt{3}sin2x-cos2x=0$,
所以$\sqrt{3}sin2x=cos2x$,
即$tan2x=\frac{{\sqrt{3}}}{3}$;
(Ⅱ) $f(x)=\overrightarrow a•\overrightarrow b=2\sqrt{3}sinxcosx-cos2x=2sin(2x-\frac{π}{6})$,
所以$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$,
即$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}(k∈Z)$,
所以f(x)的单调递增区间是$[kπ-\frac{π}{6},kπ+\frac{π}{3}](k∈Z)$.
点评 本题考查了向量的垂直问题,考查函数的单调性问题,是一道中档题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{175}{264}$ | B. | $\frac{11}{24}$ | C. | $\frac{175}{132}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
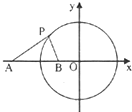 已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com