
 成等差数列,则
成等差数列,则 .
. | ξ | -1 | 0 | 1 |
| P | a | b |  |
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
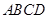 的边长为2,
的边长为2,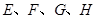 分别是边
分别是边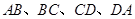 的中点.
的中点.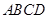 内部随机取一点
内部随机取一点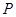 ,求满足
,求满足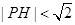 的概率;
的概率;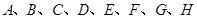 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为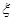 ,求随机变量
,求随机变量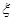 的分布列与数学期望
的分布列与数学期望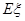 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
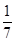 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同, 箱中没有球.我们把从
箱中没有球.我们把从 箱中取1个球放入
箱中取1个球放入 箱中,然后在
箱中,然后在 箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作. 箱中恰有1个、2个、3个白球的概率;
箱中恰有1个、2个、3个白球的概率; 箱中一次取出2个球,记白球的个数为
箱中一次取出2个球,记白球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com