
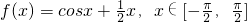 ,
,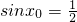 ,
,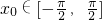 .那么下面命题中真命题的序号是
.那么下面命题中真命题的序号是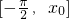 上是增函数
上是增函数 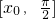 上是增函数.
上是增函数.科目:高中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)与g(x)分别由下表给出:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
1 | 2 | 3 | 4 | x |
1 | 2 | 3 | 4 |
| f(x) |
2 | 3 | 4 | 1 | g(x) |
2 | 1 | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一年级期中考试数学试卷 题型:选择题
已知函数 ,用二分法求方程
,用二分法求方程 内近似解的过程中,取区间中点
内近似解的过程中,取区间中点 ,那么下一个有根区间为 ( )
,那么下一个有根区间为 ( )
A.(1,2) B.(2,3) C.(1,2)或(2,3)都可以 D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
(本小题满分14分)
阅读下面一段文字:已知数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,则易知通项
,则易知通项![]() ,前
,前![]() 项的和
项的和![]() . 将此命题中的“等号”改为“大于号”,我们得到:数列
. 将此命题中的“等号”改为“大于号”,我们得到:数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,那么
,那么![]() ,且
,且![]() . 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证
. 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证![]() ,可以先证
,可以先证![]() ,而要证
,而要证![]() ,只需证
,只需证![]() (
(![]() ). 结合以上思想方法,完成下题:
). 结合以上思想方法,完成下题:
已知函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,若数列
,若数列![]() 的前
的前![]() 项的和为
项的和为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com