
分析 若函数f(x)有2个不同的零点,则$\frac{|x|}{x+2}$-kx2=0 ①有2个不同的实数根.再分(1)当x=0时、(2)x≠0时2种情况,分别求出方程的根,综合可得方程①有2个不相等的实数根的条件.
解答 解:若函数f(x)=$\frac{\left|x\right|}{x+2}$-kx2(k∈R)有两个零点,
则$\frac{\left|x\right|}{x+2}$-kx2=0 ①有两个不同的实数根.
(1)当x=0时,不论k取何值,方程①恒成立,即x=0恒为方程①的一个实数解.
(2)故只需x≠0,函数f(x)=$\frac{\left|x\right|}{x+2}$-kx2(k∈R)有1个零点
?$\frac{\left|x\right|}{x+2}$-kx2=0 有1个不同的实数根
?$\frac{1}{x+2}$=k|x|有1个异根,
?函数y=$\frac{1}{x+2}$与y=k|x|有1个交点,
如图示: ,
,
k>0时,由$\frac{1}{x+2}$=-kx得:kx2+2kx+1=0,
△=4k2-4k=0,解得:k=1,
结合图象,k<0或0<k<1,
故答案为:k<0或0<k<1.
点评 本题主要考查函数零点和方程的根的关系,方程根的存在性以及个数判断,二次函数的性质,体现了转化、分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{4}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
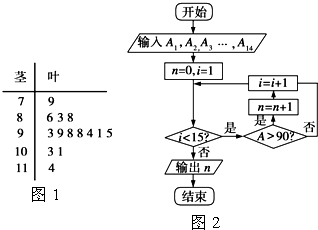 如图1是某高三学生进入高中-二年来的数学考试成绩茎叶图,第1次到第 14次.考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是10.
如图1是某高三学生进入高中-二年来的数学考试成绩茎叶图,第1次到第 14次.考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是10.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,1) | B. | (-∞,1)∪($\frac{3}{2}$,+∞) | C. | (1,$\frac{3}{2}$) | D. | (-∞,1)∪[$\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3cosx | B. | f(x)=x3+x2 | C. | f(x)=1+sin2x | D. | f(x)=ex+x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正△ABC两边AB,AC的中点分别为M,N,直线MN与△ABC外接圆的一个交点为P.
正△ABC两边AB,AC的中点分别为M,N,直线MN与△ABC外接圆的一个交点为P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com