解:(1)∵已知直线AB的斜率k与倾斜角α,∴k=tanα=
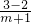
=
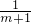
,
当m=-1时,直线的斜率不存在,倾斜角α=90°.
当m<-1时,k<0,由α∈[0°,180° ),α=180°+arctan
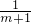
.
当m>-1时,k>0,α=arctan
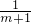
.
(2)当m=-1时,直线的斜率不存在,直线的方程为 x=-1,
当m≠-1时,由两点式求直线的方程
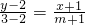
,即 x-(m+1)y+2m+3=0.
(3)已知实数m∈[-

-1,

-1],∴-

≤m+1≤

.
①当m+1≠0时,

≤
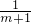
,或
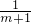
≤-

.
即 tan α≥

或tan α≤-

,
∴90°>α≥30°,或 90°<α≤120°.
②当m=-1时,直线的斜率不存在,倾斜角α=90°.
综上,α∈[30°,120°].
分析:(1)k=tanα=
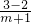
=
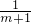
,分m=-1、m<-1、m>-1 三种情况求倾斜角α.
(2)当m=-1时,直线的斜率不存在,写出直线的方程;当m≠-1时,由两点式求直线的方程.
(3)已知实数m∈[-

-1,

-1],利用不等式的性质求出斜率tanα的范围,再利用正切函数的单调性求出
倾斜角α的范围.
点评:本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小,以及用两点式求直线的方程,体现了分类讨论的数学思想.

 -1,
-1, -1],求直线AB的倾斜角α的取值范围.
-1],求直线AB的倾斜角α的取值范围.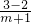 =
=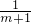 ,
,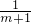 .
.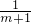 .
.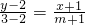 ,即 x-(m+1)y+2m+3=0.
,即 x-(m+1)y+2m+3=0. -1,
-1, -1],∴-
-1],∴- ≤m+1≤
≤m+1≤ .
. ≤
≤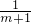 ,或
,或 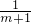 ≤-
≤- .
. 或tan α≤-
或tan α≤- ,
,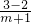 =
=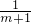 ,分m=-1、m<-1、m>-1 三种情况求倾斜角α.
,分m=-1、m<-1、m>-1 三种情况求倾斜角α. -1,
-1, -1],利用不等式的性质求出斜率tanα的范围,再利用正切函数的单调性求出
-1],利用不等式的性质求出斜率tanα的范围,再利用正切函数的单调性求出
