
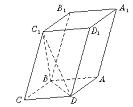
(14分)如图,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形且∠C1CB=∠C1CD=∠BCD=60°.
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1= ,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
(3)当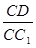 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
(1)见解析;(2)cosC1OC=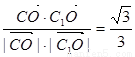 ;(3)x=1.
;(3)x=1.
【解析】
试题分析:
(1)证明:设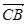 =
=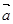 ,
,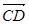 =
=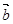 ,
,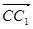 =
=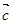 ,则|
,则|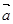 |=|
|=|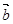 |,∵
|,∵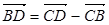 =
=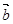 -
-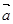 ,
,
∴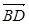 ·
·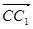 =(
=(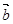 -
-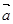 )·
)·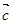 =
=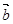 ·
·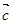 -
-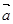 ·
·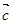 =|
=|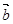 |·|
|·|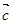 |cos60°-|
|cos60°-|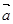 |·|
|·|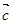 |cos60°=0,
|cos60°=0,
∴C1C⊥BD.
(2)解:连AC、BD,设AC∩BD=O,连OC1,则∠C1OC为二面角α—BD—β的平面角.
∵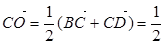 (
(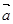 +
+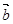 ),
),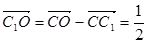 (
(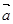 +
+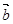 )-
)-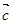
∴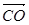 ·
·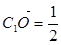 (
(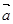 +
+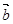 )·[
)·[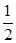 (
(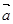 +
+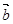 )-
)-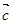 ]
]
=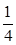 (
(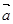 2+2
2+2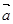 ·
·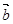 +
+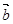 2)-
2)-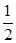
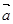 ·
·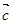 -
-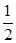
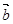 ·
·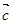
=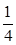 (4+2·2·2cos60°+4)-
(4+2·2·2cos60°+4)-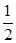 ·2·
·2·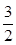 cos60°-
cos60°-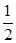 ·2·
·2·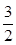 cos60°=
cos60°=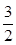 .
.
则|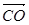 |=
|=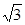 ,|
,|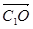 |=
|=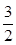 ,∴cosC1OC=
,∴cosC1OC=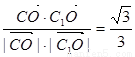
(3)解:设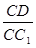 =x,CD=2, 则CC1=
=x,CD=2, 则CC1=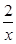 .
.
∵BD⊥平面AA1C1C,∴BD⊥A1C
∴只须求满足: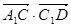 =0即可.
=0即可.
设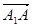 =
=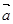 ,
,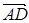 =
=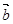 ,
,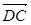 =
=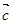 ,
,
∵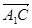 =
=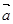 +
+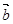 +
+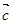 ,
,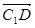 =
=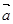 -
-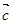 ,
,
∴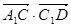 =(
=(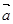 +
+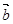 +
+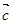 )(
)(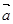 -
-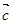 )=
)=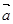 2+
2+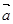 ·
·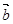 -
-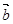 ·
·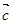 -
-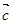 2=
2= -6,
-6,
令6-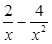 =0,得x=1或x=-
=0,得x=1或x=-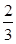 (舍去).
(舍去).
考点:本题主要考查向量的坐标运算、数量积、模的概念及计算、夹角公式的应用,考查了考生的空间想象能力、逻辑推理能力。
点评:本题蕴涵着转化思想,即用向量这个工具来研究空间垂直关系的判定、二面角的求解以及待定值的探求等问题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且| OA |
| a |
| OC |
| b |
| OO1 |
| c |
| a |
| b |
| c |
| OG |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com