|
|
|
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cos , , ∈[0, ∈[0,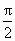 ]. ].
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l: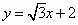 垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标. 垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,四凌锥p-ABCD中,底面ABCD为矩形,PA上面ABCD,E为PD的点.
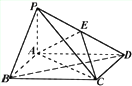
(Ⅰ)证明:PP∥平面AEC;
(Ⅱ)设置AP=1,AD=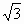 ,三凌P-ABD的体积V= ,三凌P-ABD的体积V=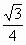 ,求A到平面PBC的距离. ,求A到平面PBC的距离.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为
|
| [ ] |
A. |
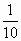
|
B. |
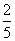
|
C. |
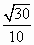
|
D. |
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,四棱锥p-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
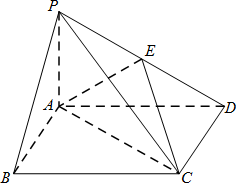
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=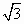 ,求三棱锥E-ACD的体积. ,求三棱锥E-ACD的体积.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若向量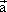 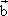 满足:| 满足:|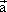 |=1,( |=1,(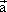 + +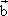 )⊥ )⊥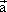 (2 (2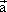 + +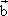 )⊥ )⊥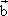 ,则| ,则|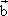 |= |=
|
| [ ] |
A. |
2
|
B. |
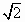
|
C. |
1
|
D. |
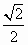
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知二面角α-l-β为60°,AB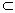 α,AB⊥l,A为垂足,CD α,AB⊥l,A为垂足,CD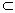 β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为 β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为
|
| [ ] |
A. |
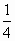
|
B. |
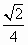
|
C. |
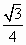
|
D. |
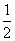
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
为了了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为
|
| [ ] |
A. |
50
|
B. |
40
|
C. |
25
|
D. |
20
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
命题“ x∈[0,+∞)x3+x≥0”的否定是 x∈[0,+∞)x3+x≥0”的否定是
|
| [ ] |
A. |
 x∈(0,∞)x3+x<0 x∈(0,∞)x3+x<0
|
B. |
 x∈(-∞,0)x3+x≥0 x∈(-∞,0)x3+x≥0
|
C. |
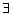 x0∈[0,+∞)x x0∈[0,+∞)x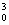 +x0≤0 +x0≤0
|
D. |
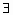 x0∈[0,+∞)x x0∈[0,+∞)x +x0≥0 +x0≥0
|
|
|
查看答案和解析>>
