|
|
|
如图,四凌锥p-ABCD中,底面ABCD为矩形,PA上面ABCD,E为PD的点.
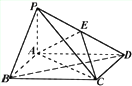
(Ⅰ)证明:PP∥平面AEC;
(Ⅱ)设置AP=1,AD=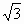 ,三凌P-ABD的体积V= ,三凌P-ABD的体积V=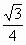 ,求A到平面PBC的距离. ,求A到平面PBC的距离.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若变量x,y满足约束条件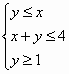 ,则z=2x+y的最大值为________. ,则z=2x+y的最大值为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
甲、乙两套设备生产的同类型产品共4800件,采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为________件.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
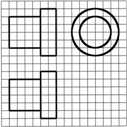
如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6c m的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为
|
| [ ] |
A. |
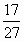
|
B. |
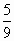
|
C. |
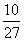
|
D. |
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
甲、已两名元动员各自等可能地从红、白、蓝3种颜色的运动服种选择1种,则他们选择相同颜色运动服的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为p=2cosθ, ∈[0, ∈[0,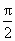 ]. ].
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l:y=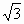 x+2垂直,根据(I)中你得到的参数方程,确定D的坐标. x+2垂直,根据(I)中你得到的参数方程,确定D的坐标.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
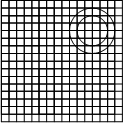
如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件有一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为
|
| [ ] |
A. |
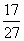
|
B. |
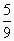
|
C. |
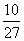
|
D. |
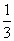
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cos , , ∈[0, ∈[0,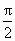 ]. ].
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l: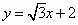 垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标. 垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2,作如图2折叠,折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.
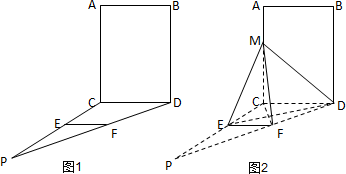
(1)证明:CF⊥平面MDF;
(2)求三棱锥M-CDE的体积.
|
|
|
查看答案和解析>>
