
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
解:由题意得f′(x)=12x2-2a.
当a≤0时,f′(x)≥0恒成立,此时f(x)的单调递增区间为(-∞,+∞).
当a>0时,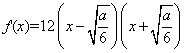 ,
,
此时函数f(x)的单调递增区间为
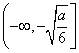 和
和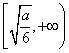 .
.
单调递减区间为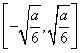 .
.
证明:由于0≤x≤1,故当a≤2时,f(x)+|a-2|=4x3-2ax+2≥4x3-4x+2.
当a>2时,f(x)+|a-2|=4x3+2a(1-x)-2≥4x3+4(1-x)-2=4x3-4x+2.
设g(x)=2x3-2x+1,0≤x≤1,
则g′(x)=6x2-2=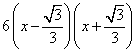 ,
,
于是在x∈(0,1)上,当x变化时,g′(x),g(x)的变化情况如下表:
| x | 0 |
|
|
| 1 |
| g′(x) | - | 0 | + | ||
| g(x) | 1 | 单调递减 | 极小值
| 单调递增 | 1 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数 ,g(x)=x2-2bx+4,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是( )
,g(x)=x2-2bx+4,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是( )
A. B.[1,+∞] C.
B.[1,+∞] C. D.[2,+∞]
D.[2,+∞]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数 下列结论中①
下列结论中① ②函数
②函数 的图象是中心对称图形 ③若
的图象是中心对称图形 ③若 是
是 的极小值点,则
的极小值点,则 在区间
在区间 单调递减 ④若
单调递减 ④若 是
是 的极值点,则
的极值点,则 . 正确的个数有( )
. 正确的个数有( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
数列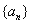 的前n项和为
的前n项和为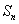 ,存在常数A,B,C,使得
,存在常数A,B,C,使得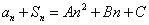 对任意正整数n都成立.
对任意正整数n都成立.
⑴若数列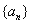 为等差数列,求证:3A-B+C=0;
为等差数列,求证:3A-B+C=0;
⑵若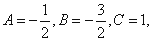 设
设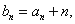 数列
数列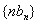 的前n项和为
的前n项和为 ,求
,求 ;
;
⑶若C=0,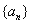 是首项为1的等差数列,设
是首项为1的等差数列,设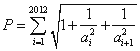 ,求不超过P的最大整数的值.
,求不超过P的最大整数的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个命题:
①  ,
, ”是全称命题;
”是全称命题;
② 命题“ ,
, ”的否定是“
”的否定是“ ,使
,使 ”;
”;
③ 若 ,则
,则 ;
;
④ 若 为假命题,则
为假命题,则 、
、 均为假命题.
均为假命题.
其中真命题的序号是( )
A.①② B.①④ C.②④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com