
如图,等边三角形OAB的边长为8 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.

(1)求抛物线E的方程;
(2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q.证明:以PQ为直径的圆恒过y轴上某定点.
(1)x2=4y.(2)见解析
【解析】(1)依题意,OB=8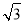 ,∠BOy=30°.设B(x,y),则x=OBsin30°=4
,∠BOy=30°.设B(x,y),则x=OBsin30°=4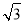 ,y=OBcos30°=12.因为点B(4
,y=OBcos30°=12.因为点B(4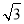 ,12)在x2=2py上,所以(4
,12)在x2=2py上,所以(4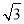 )2=2p×12,解得p=2.故抛物线E的方程为x2=4y.
)2=2p×12,解得p=2.故抛物线E的方程为x2=4y.
(2)由(1)知y=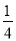 x2,y′=
x2,y′=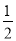 x.设P(x0,y0),
x.设P(x0,y0),
则x0≠0,y0=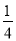
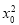 ,且l的方程为y-y0=
,且l的方程为y-y0=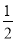 x0(x-x0),即y=
x0(x-x0),即y=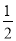 x0x-
x0x-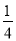
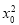 .
.
由 得
得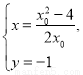 所以Q为
所以Q为 .
.
设M(0,y1),令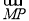 ·
·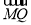 =0对满足y0=
=0对满足y0=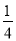
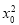 (x0≠0)的x0,y0恒成立.
(x0≠0)的x0,y0恒成立.
由于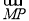 =(x0,y0-y1),
=(x0,y0-y1),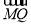 =
= ,
,
由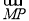 ·
·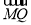 =0,得
=0,得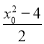 -y0-y0y1+y1+
-y0-y0y1+y1+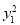 =0,即(
=0,即(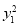 +y1-2)+(1-y1)y0=0.(*)
+y1-2)+(1-y1)y0=0.(*)
由于(*)式对满足y0=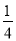
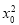 (x0≠0)的y0恒成立,所以
(x0≠0)的y0恒成立,所以 解得y1=1.
解得y1=1.
故以PQ为直径的圆恒过y轴上的定点M(0,1).


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第6课时练习卷(解析版) 题型:填空题
一高考考生咨询中心有A、B、C三条咨询热线.已知某一时刻热线A、B占线的概率均为0.5,热线C占线的概率为0.4,各热线是否占线相互之间没有影响,假设该时刻有ξ条热线占线,则随机变量ξ的期望为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第4课时练习卷(解析版) 题型:填空题
下列问题属于超几何分布的有________.(填序号)
①抛掷三枚骰子,所得向上的数是6的骰子的个数记为X,求X的概率分布列;
②有一批种子的发芽率为70%,现任取10颗种子做发芽实验,把实验中发芽的种子的个数记为X,求X的概率分布列;
③一盒子中有红球3只,黄球4只,蓝球5只,现任取3只球,把不是红色的球的个数记为X,求X的概率分布列;
④某班级有男生25人,女生20人,现选派4名学生参加学校组织的活动,班长必须参加,其中女生人数记为X,求X的概率分布列.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第3课时练习卷(解析版) 题型:填空题
在(x+y)n的展开式中,若第七项系数最大,则n的值可能为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第9课时练习卷(解析版) 题型:填空题
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C.若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第9课时练习卷(解析版) 题型:解答题
抛物线y2=2px的准线方程为x=-2,该抛物线上的每个点到准线x=-2的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线l1:y=x和l2:y=-x相切的圆,
(1)求定点N的坐标;
(2)是否存在一条直线l同时满足下列条件:
①l分别与直线l1和l2交于A、B两点,且AB中点为E(4,1);
②l被圆N截得的弦长为2.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第9课时练习卷(解析版) 题型:填空题
抛物线y=ax2的准线方程是y=2,则a的值是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第8课时练习卷(解析版) 题型:解答题
已知双曲线 =1(a>0,b>0)的两条渐近线方程为y=±
=1(a>0,b>0)的两条渐近线方程为y=± x,若顶点到渐近线的距离为1,求双曲线方程.
x,若顶点到渐近线的距离为1,求双曲线方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第6课时练习卷(解析版) 题型:填空题
在平面直角坐标系中,有椭圆 =1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆.过点
=1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆.过点 作圆的两切线互相垂直,则离心率e=________.
作圆的两切线互相垂直,则离心率e=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com