
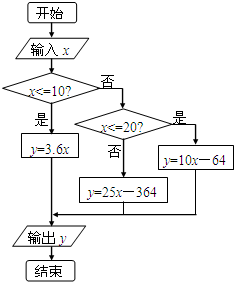
 (2009•台州二模)某个缺水地区为了提倡居民节约用水和控制用水浪费现象,实行了水费的分段计价,其计价的流程如图所示.其中输入为居民每月的用水量(单位:吨),输出为相应的水费(单位:元).已知某户居民某月用水量为x(x>20)吨,则该户居民用水超过20吨的部分应缴纳的水费为
(2009•台州二模)某个缺水地区为了提倡居民节约用水和控制用水浪费现象,实行了水费的分段计价,其计价的流程如图所示.其中输入为居民每月的用水量(单位:吨),输出为相应的水费(单位:元).已知某户居民某月用水量为x(x>20)吨,则该户居民用水超过20吨的部分应缴纳的水费为

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| a |
| b |
| b |
| a |
| c |
| b |
| c |
| b |
| c |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com