
7.(2014高考北京卷)设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间[ ,
, ]上具有单调性,且f(
]上具有单调性,且f( )=f(
)=f(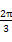 )=-f(
)=-f( ),则f(x)的最小正周期为 .
),则f(x)的最小正周期为 .
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
有下列命题:
①若sin α>0,则角α是第一、二象限角;②若角α是第二象限角,且P(x,y)是其终边上一点,则cos α=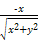 ;③若sin α=sin β,则α与β的终边相同;④第二象限角大于第一象限角.
;③若sin α=sin β,则α与β的终边相同;④第二象限角大于第一象限角.
其中错误命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=cos x(sin x+cos x)- .
.
(1)若0<α< ,且sin α=
,且sin α= ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知D、E、F分别为△ABC的边BC、CA、AB的中点,且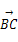 =a,
=a,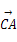 =b,给出下列命题:①
=b,给出下列命题:①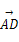 =
= a-b;②
a-b;②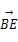 =a+
=a+ b;③
b;③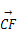 =-
=- a+
a+ b;④
b;④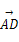 +
+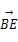 +
+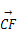 =0.
=0.
其中正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com