
已知函数f(x)=cos x(sin x+cos x)- .
.
(1)若0<α< ,且sin α=
,且sin α= ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
解:法一 (1)因为0<α< ,sin α=
,sin α= ,
,
所以cos α= .
.
所以f(α)= (
( +
+ )-
)- =
= .
.
(2)因为f(x)=sin xcos x+cos2x-
= sin 2x+
sin 2x+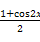 -
-
= sin 2x+
sin 2x+ cos 2x
cos 2x
= sin(2x+
sin(2x+ ),
),
所以T=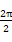 =π.
=π.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得kπ-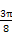 ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
所以f(x)的单调递增区间为[kπ-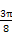 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
法二 f(x)=sin xcos x+cos2x-
= sin 2x+
sin 2x+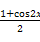 -
-
= sin 2x+
sin 2x+ cos 2x
cos 2x
= sin(2x+
sin(2x+ ).
).
(1)因为0<α< ,sin α=
,sin α= ,
,
所以α= ,
,
从而f(α)= sin(2α+
sin(2α+ )=
)= sin
sin 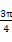 =
= .
.
(2)T=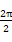 =π.
=π.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得kπ-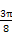 ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
所以f(x)的单调递增区间为[kπ-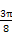 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
7.(2014高考北京卷)设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间[ ,
, ]上具有单调性,且f(
]上具有单调性,且f( )=f(
)=f(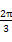 )=-f(
)=-f( ),则f(x)的最小正周期为 .
),则f(x)的最小正周期为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
为了得到函数y=sin(2x+1)的图象,只需把函数y=sin 2x的图象上所有的点( )
(A)向左平行移动 个单位长度
个单位长度
(B)向右平行移动 个单位长度
个单位长度
(C)向左平行移动1个单位长度
(D)向右平行移动1个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos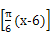 (x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为 ℃.
(x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为 ℃.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点A(-1,5)和向量a=(2,3),若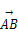 =3a,则点B的坐标为( )
=3a,则点B的坐标为( )
(A)(7,4) (B)(7,14) (C)(5,4) (D)(5,14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com