练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数sin α-cos α=-(0<α<),则α属于(　　)

    (A)(0,)    (B)(,)

    (C)(,) (D)(,)


    B解析:sin α-cos α=sin(α-)=-,

    sin(α-)=-,由-<-<0,

    因为0<α<,

    所以-<α-<0,即<α<,


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    7.(2014高考北京卷)设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间[,]上具有单调性,且f(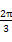)=f()=-f(),则f(x)的最小正周期为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos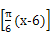(x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为　　　　℃. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=Asin(ωx+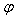)(x∈R,A>0,ω>0,0<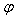<)的部分图象如图所示,P是图象的最高点,Q为图象与x轴的交点,O为坐标原点.若OQ=4,OP=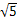,PQ=.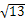

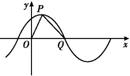
    (1)求函数y=f(x)的解析式;

    (2)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,当x∈[0,3]时,求函数h(x)=f(x)·g(x)的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知cos α=,cos(α+β)=-,α∈(0,),α+β∈(,π),则β的值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3,).

    (1)求sin 2α-tan α的值;

    (2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数y=f(-2x)-2f2(x)在区间[0,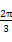]上的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列命题:

    ①两个具有公共终点的向量,一定是共线向量.

    ②两个向量不能比较大小,但它们的模能比较大小.

    ③λa=0(λ为实数),则λ必为零.

    其中错误的命题的个数为(　　)

    (A)1    (B)2    (C)3    (D)0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61,

    (1)求a与b的夹角θ;

    (2)求|a+b|;

    (3)若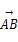=a,=b,求△ABC的面积.

    查看答案和解析>>

    同步练习册答案