
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3, ).
).
(1)求sin 2α-tan α的值;
(2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数y= f(
f( -2x)-2f2(x)在区间[0,
-2x)-2f2(x)在区间[0,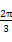 ]上的值域.
]上的值域.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
有下列命题:
①若sin α>0,则角α是第一、二象限角;②若角α是第二象限角,且P(x,y)是其终边上一点,则cos α=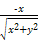 ;③若sin α=sin β,则α与β的终边相同;④第二象限角大于第一象限角.
;③若sin α=sin β,则α与β的终边相同;④第二象限角大于第一象限角.
其中错误命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,长为3.5 m的木棒AB斜靠在石堤旁,木棒的一端A在离堤足C处1.4 m的地面上,另一端B在离堤足C处2.8 m的石堤上,石堤的倾斜角为α,则坡度值tan α等于()

(A)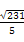 (B)
(B)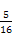 (C)
(C)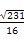 (D)
(D)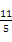
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在平面四边形ABCD中,AD=1,CD=2,
AC=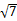 .
.
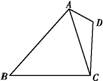
(1)求cos ∠CAD的值;
(2)若cos ∠BAD=-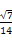 ,sin ∠CBA=
,sin ∠CBA=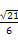 ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知D、E、F分别为△ABC的边BC、CA、AB的中点,且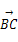 =a,
=a,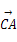 =b,给出下列命题:①
=b,给出下列命题:①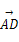 =
= a-b;②
a-b;②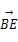 =a+
=a+ b;③
b;③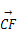 =-
=- a+
a+ b;④
b;④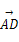 +
+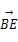 +
+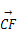 =0.
=0.
其中正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com