
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,BQ⊥AD,线段PC上是否存在点M,使得PA∥平面MQB?
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,BQ⊥AD,线段PC上是否存在点M,使得PA∥平面MQB? 分析 连接AC交BQ于N,连接MN,由相似三角形可得$\frac{AN}{AC}=\frac{1}{3}$,故当$\frac{PM}{PC}=\frac{1}{3}$时,PA∥MN,于是PA∥平面MQB.
解答 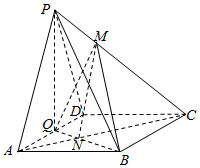 解:当M为PC的靠近P的三等分点时,PA∥平面MQB.
解:当M为PC的靠近P的三等分点时,PA∥平面MQB.
证明如下:连接AC交BQ于N,连接MN.
∵∠BAD=60°,BQ⊥AD,
∴AQ=ABcos60°=$\frac{1}{2}$AB=$\frac{1}{2}AD$,
∴Q为AD的中点.
∵AQ∥BC,
∴△AQN∽△CBN,
∴$\frac{AN}{CN}=\frac{AQ}{BC}$=$\frac{1}{2}$,
∴$\frac{AN}{AC}=\frac{1}{3}$.又$\frac{PM}{PC}$=$\frac{1}{3}$,
∴$\frac{AN}{AC}=\frac{PM}{PC}$,∴MN∥PA,
又MN?平面MQB,PA?平面MQB,
∴PA∥平面MQB.
点评 本题考查了线面平行的判定,计算$\frac{AN}{AC}$是确定M点位置的关键,属于中档题,


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
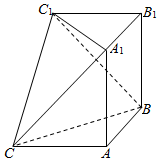 如图,AA1,BB1均垂直于平面ABC和平面A1B1C1,∠BAC=∠A1B1C1=90°,AC=AB=A1A=B1C1=$\sqrt{2}$,则多面体ABC-A1B1C1的外接球的表面积为( )
如图,AA1,BB1均垂直于平面ABC和平面A1B1C1,∠BAC=∠A1B1C1=90°,AC=AB=A1A=B1C1=$\sqrt{2}$,则多面体ABC-A1B1C1的外接球的表面积为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 以上都可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )
定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )| A. | $\frac{{2-\sqrt{3}}}{4}$ | B. | $\frac{{2+\sqrt{3}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com