
(本小题12分)如图,已知直角梯形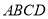 中,
中,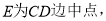 且
且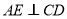 ,又
,又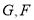 分别为
分别为 的中点,将△
的中点,将△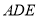 沿
沿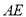 折叠,使得
折叠,使得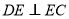 .
.

(Ⅰ)求证:AE⊥平面CDE;
(Ⅱ)求证:FG∥平面BCD;
(Ⅲ)在线段AE上找一点R,使得平面BDR⊥平面DCB, 并说明理由.
(Ⅰ)(Ⅱ)(Ⅲ)见解析
【解析】
试题分析:(Ⅰ)(Ⅱ)利用判定定理证明线面平行时,关键是在平面内找一条与已知直线平行的直线,解题时可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过平行线分线段成比例等.证明直线和平面垂直的常用方法:(1)利用判定定理.(2)利用判定定理的推论.(3)利用面面平行的性质.(4)利用面面垂直的性质.(Ⅲ)判定面面垂直的方法(1)面面垂直的定义,即证两平面所成的二面角为直角;(2)面面垂直的判定定理
试题解析:(1)由已知得DE⊥AE,AE⊥EC.
∵DE∩EC=E,DE、EC?平面DCE. 2分
∴AE⊥平面CDE. 4分
(2)取AB中点H,连接GH、FH,
∴GH∥BD,FH∥BC,

又GH∩FH=H,
∴平面FHG∥平面BCD, 7分

∴GF∥平面BCD. 8分
(3)取线段AE的中点R,则平面BDR⊥平面DCB
取线段DC的中点M,取线段DB中点H,连接MH,RH,BR,DR
在△DEC中,


∵M为线段DC,H为线段DB中点,R为线段AE中点
 又
又 ,
,
∴ RH⊥DC 10分




∴ RH⊥面DCB 11分
∵ RH?平面DRB
平面DRB⊥平面DCB
即 取AE中点R时,有平面DBR⊥平面DCB 12分
(其它正确答案请酌情给分)
考点:立体几何综合应用


科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
设椭圆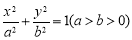 的离心率为
的离心率为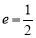 ,右焦点为F(c,0),方程
,右焦点为F(c,0),方程 的两个实根分别为x1和x2,则点P(x1,x2)的位置( )
的两个实根分别为x1和x2,则点P(x1,x2)的位置( )
A.必在圆 内
内
B.必在圆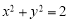 上
上
C.必在圆 外
外
D.以上三种情形都有可能
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:填空题
如图,直三棱柱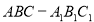 的侧棱长和底面边长均为2,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为__________.
的侧棱长和底面边长均为2,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为__________.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:选择题
用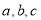 表示三条不同的直线,
表示三条不同的直线, 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ;
;
②若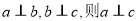 ;
;
③若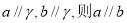 ;
;
④若 则
则 .
.
其中真命题的序号是( )
A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:填空题
已知平面 和直线
和直线 则满足下列条件中__________(填上所有正确的序号)能使
则满足下列条件中__________(填上所有正确的序号)能使 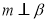 成立.
成立.
①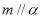 ,②
,② ;③
;③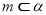 ;④
;④ .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:选择题
用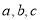 表示三条不同的直线,
表示三条不同的直线,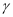 表示平面,
表示平面,
给出下列命题,其中说法正确命题的序号是( )
①若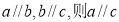 ;
;
②若 ;
;
③若 ;
;
④若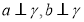 则
则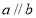 .
.
A.①② B.②③ C.①④ D.③④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试文科数学试卷(解析版) 题型:填空题
某单位有职工200名,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第5组抽出的号码为23,则第10组抽出的号码应是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com