
用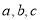 表示三条不同的直线,
表示三条不同的直线,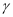 表示平面,
表示平面,
给出下列命题,其中说法正确命题的序号是( )
①若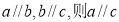 ;
;
②若 ;
;
③若 ;
;
④若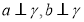 则
则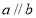 .
.
A.①② B.②③ C.①④ D.③④
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,四棱锥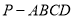 中,
中,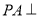 平面
平面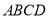 ,
,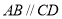 ,
,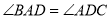
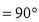 ,
, ,
,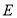 为
为 的中点.
的中点.

(Ⅰ)证明: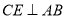 ;
;
(Ⅱ)若二面角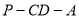 为
为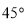 ,求直线
,求直线 与平面
与平面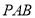 所成角的正切值.
所成角的正切值.
(Ⅲ)若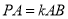 ,求平面
,求平面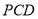 与平面PAB所成的锐二面角的余弦值
与平面PAB所成的锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:解答题
(本小题12分)已知平行四边形 的三个顶点的坐标为
的三个顶点的坐标为 ,
,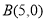 ,
,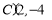 .
.
(Ⅰ)在 ABC中,求边AC中线所在直线方程;
ABC中,求边AC中线所在直线方程;
(Ⅱ)求的顶点 的坐标及对角线
的坐标及对角线 的长度;
的长度;
(Ⅲ)求平行四边形 的面积及边AD所在的直线方程.
的面积及边AD所在的直线方程.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:解答题
(本小题12分)如图,已知直角梯形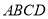 中,
中,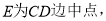 且
且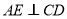 ,又
,又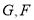 分别为
分别为 的中点,将△
的中点,将△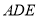 沿
沿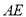 折叠,使得
折叠,使得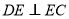 .
.

(Ⅰ)求证:AE⊥平面CDE;
(Ⅱ)求证:FG∥平面BCD;
(Ⅲ)在线段AE上找一点R,使得平面BDR⊥平面DCB, 并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古一机一中高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)已知函数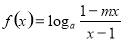 是奇函数(
是奇函数( 且
且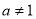 ).
).
①求实数 的值;
的值;
②判断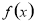 在区间
在区间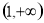 上的单调性,并加以证明;
上的单调性,并加以证明;
③当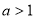 且
且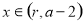 时,
时, 的值域是
的值域是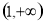 ,求实数
,求实数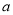 与
与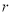 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高二上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分15分)今年的国庆假期是实施免收小型客车高速通行费后的第一个重大节假日,有一个自驾游车队。该车队是由31辆车身长都约为5m(以5m计算)的同一车型组成的,行程中经过一个长为2725m的隧道(通过该隧道的车速不能超过25m/s),若车队匀速通过该隧道,设车队的速度为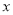 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当 时,相邻两车之间保持20m的距离;当
时,相邻两车之间保持20m的距离;当 时,相邻两车之间保持
时,相邻两车之间保持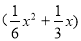 m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为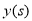 .
.
(1)将 表示为
表示为 的函数;
的函数;
(2)求该车队通过隧道时间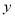 的最小值及此时车队的速度.
的最小值及此时车队的速度.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省湛江市高一上学期期中考试数学试卷(解析版) 题型:解答题
(满分14分)设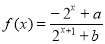 (
( 为实常数)。
为实常数)。
(1)当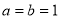 时,证明:①
时,证明:①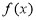 不是奇函数;
不是奇函数;
② 是
是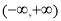 上的单调递减函数。
上的单调递减函数。
(2)设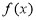 是奇函数,求
是奇函数,求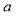 与
与 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com