
(本题满分12分)已知函数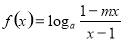 是奇函数(
是奇函数( 且
且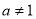 ).
).
①求实数 的值;
的值;
②判断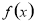 在区间
在区间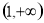 上的单调性,并加以证明;
上的单调性,并加以证明;
③当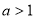 且
且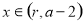 时,
时, 的值域是
的值域是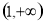 ,求实数
,求实数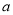 与
与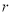 的值.
的值.
①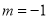 ;②;当
;②;当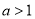 时,
时,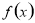 在
在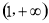 上是减函数;当
上是减函数;当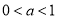 时,
时,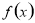 在
在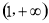 上是增函数;③
上是增函数;③ .
.
【解析】
试题分析:本题以复合对数函数为载体,综合考查对数函数的性质,函数的单调性,函数的奇偶性,对考生数学式子变形能力要求较高.(1)由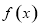 为奇函数,根据
为奇函数,根据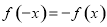 可以求出
可以求出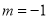 ;(2)证明函数的单调性要利用定义:任意取值—作差—变形—定号下结论,在作差变形后得到的时对数式,再作差比较真数和1的大小,由于
;(2)证明函数的单调性要利用定义:任意取值—作差—变形—定号下结论,在作差变形后得到的时对数式,再作差比较真数和1的大小,由于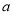 不确定,还需要分
不确定,还需要分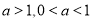 两种情况讨论函数的单调性;(3)函数的定义域为
两种情况讨论函数的单调性;(3)函数的定义域为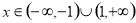 ,所以
,所以 ,由题意
,由题意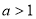 ,所以
,所以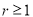 ,又
,又 时,解得
时,解得 ,由(2)知函数
,由(2)知函数 在
在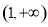 上为减函数,要满足
上为减函数,要满足 的值域是
的值域是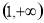 ,需要
,需要 时,
时, ,所以
,所以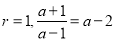 即
即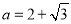 .
.
试题解析:(1)因为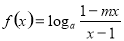 是奇函数,即
是奇函数,即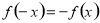 ,
,
所以 对定义域内的一切
对定义域内的一切 都成立,所以
都成立,所以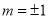 ,
,
又当 时,
时, 无意义,故
无意义,故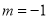
由(1)得,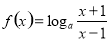 ,任意取
,任意取 且
且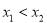 ,
,
则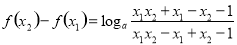 .
.
由于
因为 ,所以
,所以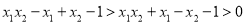 ,
,
所以
所以当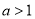 时 ,
时 , ;当
;当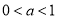 时,
时,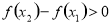 .
.
综上所述:当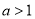 时,
时,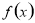 在
在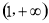 上是减函数;
上是减函数;
当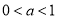 时,
时,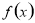 在
在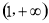 上是增函数
上是增函数
(3)由 得
得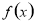 中
中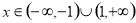 .又
.又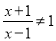 得
得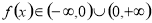
令 ,则
,则 ,解得
,解得 .所以
.所以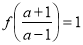 .
.
当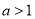 时,
时,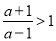 ,此时
,此时 在
在 上是减函数,
上是减函数,
所以当 时,
时, .由题意知
.由题意知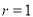 ,
,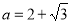 .
.
综上所述 
考点:1.对数函数的性质;2.函数的单调性


科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
如图所示,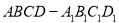 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
①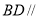 平面
平面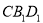 ;
;
②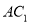 ⊥平面
⊥平面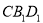 ;
;
③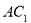 与底面
与底面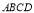 所成角的正切值是
所成角的正切值是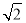 ;
;
④二面角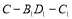 的正切值是
的正切值是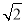 ;
;
⑤过点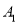 且与异面直线
且与异面直线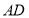 和
和 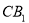 均成70°角的直线有2条.
均成70°角的直线有2条.
其中,所有正确结论的序号为________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:填空题
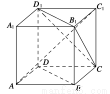
如图,直三棱柱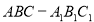 的侧棱长和底面边长均为2,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为__________.
的侧棱长和底面边长均为2,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为__________.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:填空题
已知平面 和直线
和直线 则满足下列条件中__________(填上所有正确的序号)能使
则满足下列条件中__________(填上所有正确的序号)能使 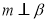 成立.
成立.
①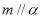 ,②
,② ;③
;③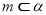 ;④
;④ .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:选择题
用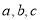 表示三条不同的直线,
表示三条不同的直线,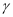 表示平面,
表示平面,
给出下列命题,其中说法正确命题的序号是( )
①若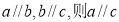 ;
;
②若 ;
;
③若 ;
;
④若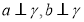 则
则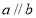 .
.
A.①② B.②③ C.①④ D.③④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省湛江市高一上学期期中考试数学试卷(解析版) 题型:填空题
若函数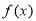 满足:存在非零常数
满足:存在非零常数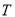 ,对定义域内的任意实数
,对定义域内的任意实数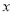 ,有
,有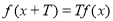 成立,则称
成立,则称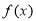 为“
为“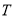 周期函数”,那么有函数①
周期函数”,那么有函数① 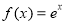 ②
② ③
③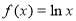 ④
④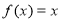 ,其中是“
,其中是“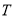 周期函数”的有 (填上所有符合条件的函数前的序号)
周期函数”的有 (填上所有符合条件的函数前的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com