
如图所示,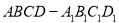 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
①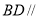 平面
平面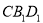 ;
;
②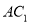 ⊥平面
⊥平面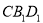 ;
;
③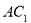 与底面
与底面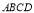 所成角的正切值是
所成角的正切值是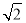 ;
;
④二面角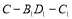 的正切值是
的正切值是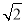 ;
;
⑤过点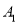 且与异面直线
且与异面直线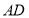 和
和 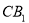 均成70°角的直线有2条.
均成70°角的直线有2条.
其中,所有正确结论的序号为________.
①②④
【解析】
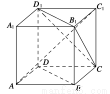
试题分析:如下图,正方体ABCD﹣A1B1C1D1 中,
由于BD∥B1D1 ,由直线和平面平行的判定定理可得BD∥平面CB1D1 ,故①正确.
由正方体的性质可得B1D1⊥A1C1,CC1⊥B1D1,故B1D1⊥平面 ACC1A1,故 B1D1⊥AC1.
同理可得 B1C⊥AC1.再根据直线和平面垂直的判定定理可得,AC1⊥平面CB1D1 ,故②正确.
AC1与底面ABCD所成角的正切值为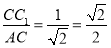 ,故③不正确.
,故③不正确.
取B1D1 的中点M,则∠CMC1 即为二面角C﹣B1D1﹣C1的平面角,Rt△CMC1中,tan∠CMC1= ,故④正确.
,故④正确.
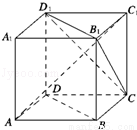
如下图,由于异面直线AD与CB1成45°的二面角,过A1 作MN∥AD、PQ∥CB1,设MN与PQ确定平面α,∠PA1M=45°,过A1 在面α上方作射线A1H,
则满足与MN、PQ 成70°的射线A1H有4条:满足∠MA1H=∠PA1H=70°的有一条,满足∠PA1H=∠NA1H=70°的有一条,满足∠NA1H=∠QA1H=70°的有一条,
满足QA1H=∠MA1H=70°的有一条.故满足与MN、PQ 成70°的直线有4条,故过点A1与异面直线AD与CB1成70°角的直线有4条,故⑤不正确.

故答案为 ①②④.
考点:二面角的定义及求法;直线和平面平行的判定;直线和平面垂直的判定;异面直线的判定.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试文科数学试卷(解析版) 题型:解答题
如图,在四棱锥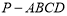 中,底面
中,底面 是菱形,且
是菱形,且 .
.
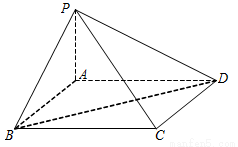
(1)求证: ;
;
(2)若平面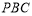 与平面
与平面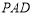 的交线为
的交线为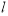 ,求证:
,求证: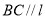 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
直线 不经过坐标原点O,且与椭圆
不经过坐标原点O,且与椭圆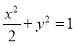 交于A、B两点,M是线段AB的中点.那么,直线AB与直线OM的斜率之积为 ( )
交于A、B两点,M是线段AB的中点.那么,直线AB与直线OM的斜率之积为 ( )
A.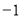 B.1 C.
B.1 C.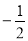 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,四棱锥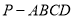 中,
中,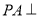 平面
平面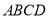 ,
,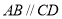 ,
,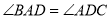
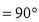 ,
, ,
, 为
为 的中点.
的中点.

(Ⅰ)证明: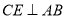 ;
;
(Ⅱ)若二面角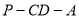 为
为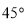 ,求直线
,求直线 与平面
与平面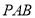 所成角的正切值.
所成角的正切值.
(Ⅲ)若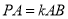 ,求平面
,求平面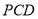 与平面PAB所成的锐二面角的余弦值
与平面PAB所成的锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
下表是一位母亲给儿子作的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据,她建立了身高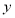 (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为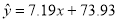 ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是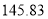 cm;
cm;
④儿子年龄增加1周岁,身高约增加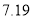 cm.
cm.
其中,正确结论的个数是
A.1 B.2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
若△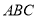 的三个内角满足
的三个内角满足 ,则△
,则△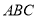
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形,也可能是钝角三角形
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古一机一中高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)已知函数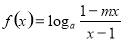 是奇函数(
是奇函数( 且
且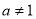 ).
).
①求实数 的值;
的值;
②判断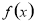 在区间
在区间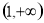 上的单调性,并加以证明;
上的单调性,并加以证明;
③当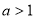 且
且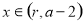 时,
时, 的值域是
的值域是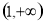 ,求实数
,求实数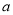 与
与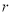 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com