【答案】
分析:①原曲线即为线x
2-(y-1)
2=1,按向量平移即是把函数向右平移1个单位,向下平移2个单位后得到曲线.
②不正确.若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离;
③充分利用平面几何图形的条件特点,结合椭圆的定义,得到|F
1Q|为定长,从而确定动点Q的轨迹是个什么图形.
④以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,先设P(x,y),欲动点P的轨迹C的方程,即寻找x,y之间的关系,结合向量的坐标运算即可得到.
⑤由题设条件将点P到平面ABC距离与到点V的距离相等转化成在面VBC中点P到V的距离与到定直线BC的距离比是一个常数,依据圆锥曲线的第二定义判断出其轨迹的形状.
解答:解:①原曲线即为x
2-(y-1)
2=1,则平移后的曲线C为(x-1)
2-(y+1)
2=1;①不正确.
②若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离.当|k|大于A、B为两个定点间的距离时动点P的轨迹不是双曲线.错;
③∵|PF
1|+|PF
2|=2a,|PQ|=|PF
2|,
∴|PF
1|+|PF
2|=|PF
1|+|PQ|=2a,
即|F
1Q|=2a,
∴动点Q到定点F
1的距离等于定长2a,故动点Q的轨迹是圆.故答案:圆.正确;
④以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,
设A(-a,0),B(a,0),P(x,y),
则
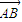
=(2a,0),
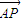
=(x+a,y),
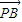
=(a-x,-y),代入
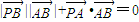
得
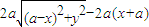
=0;
整理得y
2=4ax,
故点P的轨迹是抛物线(除去与直线AB的交点),
故错.
⑤正四面体V-ABC∴面VBC不垂直面ABC,过P作PD⊥面ABC于D,过D作DH⊥BC于H,连接PH,
可得BC⊥面DPH,所以BC⊥PH,故∠PHD为二面角V-BC-A的平面角令其为θ
则Rt△PGH中,|PD|:|PH|=sinθ(θ为S-BC-A的二面角).
又点P到平面ABC距离与到点V的距离相等,即|PV|=|PD|
∴|PV|:|PH|=sinθ<1,即在平面VBC中,点P到定点V的距离与定直线BC的距离之比是一个常数sinθ,
面VBC不垂直面ABC,所以θ是锐角,故常数sinθ<1
故由椭圆定义知P点轨迹为椭圆在面SBC内的一部分.故正确.
故答案为:③⑤
点评:本题主要考查了曲线的平移,向量共线的坐标表示,直线与椭圆的相交关系的综合应用,试题的思路比较清晰,但需要考生具备一定的运算能力及逻辑推理能力.本题中求轨迹方程的方法及定义法.定义法:若动点轨迹的条件符合某一基本轨迹的定义(如椭圆、双曲线、抛物线、圆等),可用定义直接探求.

 平移可得曲线(x+1)2-(y-3)2=1;
平移可得曲线(x+1)2-(y-3)2=1; ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 与
与 夹角为锐角θ,且满足
夹角为锐角θ,且满足  ,则点P的轨迹是圆(除去与直线AB的交点);
,则点P的轨迹是圆(除去与直线AB的交点);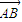 =(2a,0),
=(2a,0),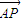 =(x+a,y),
=(x+a,y),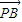 =(a-x,-y),代入
=(a-x,-y),代入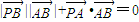 得
得 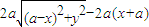 =0;
=0;
